
老板:来了,老弟!
我:来了来了。
老板:今天你要去看看KNN了,然后我给你安排一个工作!
我:好嘞!就是第二章吗?
老板:对!去吧!
可恶的老板又给我安排任务了!
《机器学习实战》这本书中的第二章为我们介绍了K-近邻算法,这是本书中第一个机器学习算法,它非常有效而且易于掌握,所以可以算是入门级算法了。
那我们现在就一起去学习一下!
简单的说,k-近邻算法采用测量不同特征值之间的距离进行分类。
其工作原理是:
其实,光看概念,还是比较抽象的。那么接下来,我们来看一个例子(原谅我思维没有那么丰富,就给大家说一下书中的例子吧,但我稍微做了一些修改,使其更形象一些)。书中的例子也不难,就是一个简单的电影题材分类问题。
老板:小韩啊,看完KNN的原理了吧?
我:看完了!
老板:那我先给你一个简单的任务。
我:≧ ﹏ ≦
老板:你先去预测一下新上映的电影《诺手的爱情》是什么题材的。
我:(啥,这是什么鬼?)没问题没问题!
老板给了一个已知电影题材的数据集,这也就是我们的训练样本集,其中只有两种类型的电影:爱情片和动作片。好,第一步,我们先来看看数据:
| 电影名称 | 打斗镜头 | 接吻镜头 | 电影类型 |
|---|---|---|---|
| 盖伦的爱情 | 3 | 104 | 爱情片 |
| 盖伦的爱情2 | 2 | 100 | 爱情片 |
| 盖伦的爱情3 | 1 | 81 | 爱情片 |
| 诺手VS奥特曼 | 101 | 10 | 动作片 |
| 诺手VS葫芦娃 | 99 | 5 | 动作片 |
| 诺手VS猪猪侠 | 98 | 2 | 动作片 |
| 诺手的爱情 | 18 | 90 | ??? |
? 我们现在知道每部电影的两个特征,一个是打斗镜头次数,一个是接吻镜头次数。那么,根据KNN的原理,我们就需要计算《盖伦VS诺手》,也就是未知电影与样本集中其他电影的距离。我们先不看怎么计算距离(后面算会提供),我们先来看结果。
| 电影名称 | 与未知电影的距离 |
|---|---|
| 盖伦的爱情 | 20.5 |
| 盖伦的爱情2 | 18.7 |
| 盖伦的爱情3 | 19.2 |
| 诺手VS奥特曼 | 115.3 |
| 诺手VS葫芦娃 | 117.4 |
| 诺手VS猪猪侠 | 118.9 |
? 好了,经过一番计算,我们得到了样本集中所有电影与未知电影的距离,按照距离递增排序,可以找到k个距离最近的电影。
? 我们假设k=3,那么距离最近的三部电影分别是:盖伦的爱情,盖伦的爱情2,盖伦的爱情3。这三部电影都是爱情片,所以我们判定《诺手的爱情》是爱情片!
Bingo!!!老板说,加鸡腿!!!
好了,老板也加鸡腿了,流程也走完了,放假了!!!等等,好像少了点啥???少了代码怎么行!!!
老板布置了新的任务,用Python代码实现K-近邻算法。没事,不要慌,慢慢来
首先,新建一个名为kNN.py的文件,写入以下代码:
from numpy import *
import operator
def createDataSet():
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
labels = [‘A‘, ‘A‘, ‘B‘, ‘B‘]
return group, labels在上面的代码中,我们导入了两个模块:第一个是科学计算包NumPy;第二个是运算符模块,k-近邻算法执行排序操作时将使用这个模块提供的函数。
createDataSet()函数,顾名思义,我们可以看出,这个函数用来创建数据集,与此同时,也创建了对应的标签。group就是我们的数据集,而每一条数据对应的类别标签就是labels。
接下来,写好代码后,我们先测试一下。不管你用什么电脑,我们都先进入python交互式环境,然后输入下列命令导入上面编辑的程序模块:
>>> import kNN然后,我们继续输入以下命令,创建两个变量,分别代表数据集和标签。
>>> group, labels = kNN.createDataSet()在python命令提示符下,输入变量的名字以检验是否正确的定义变量:
>>> group
array([[1. , 1.1],
[1. , 1. ],
[0. , 0. ],
[0. , 0.1]])>>> labels
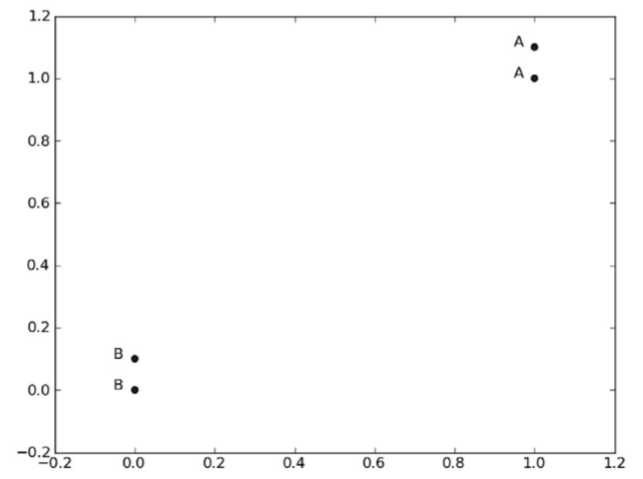
[‘A‘, ‘A‘, ‘B‘, ‘B‘]这里定义了4组数据,每组数据有两个我们已知的属性或者特征值。上面的group矩阵每行包含一个不同的数据,由于人类大脑的限制, 我们通常只能可视化处理三维以下的事务。因此为了简单地实现数据可视化,对于每个数据点我 们通常只使用两个特征。
向量labels包含了每个数据点的标签信息,labels包含的元素个数等于group矩阵行数。这里我们将数据点(1, 1.1)定义为类A,数据点(0, 0.1)定义为类B。为了说明方便,例子中的数值是任意选择的,并没有给出轴标签,图2-2是带有类标签信息的四个数据点。
表格形式:
| 数据点 | 特征1 | 特征2 | 类别 |
|---|---|---|---|
| 1 | 1.0 | 1.1 | A |
| 2 | 1.0 | 1.0 | A |
| 3 | 0 | 0 | B |
| 4 | 0 | 0.1 | B |
图表形式(引用书中内容):
好了,我们已经知道了Python如何解析数据、加载数据以及kNN算法的工作原理,接下来我们就用这些方法编写KNN分类算法。
首先,我们先来看一下k-近邻算法的伪代码:
对未知类别属性的数据集中的每个点依次执行以下操作:
(1) 计算已知类别数据集中的点与当前点之间的距离;
(2) 按照距离递增次序排序;
(3) 选取与当前点距离最小的k个点;
(4) 确定前k个点所在类别的出现频率;
(5) 返回前k个点出现频率最高的类别作为当前点的预测分类。 然后,我们再来看一下实际的Python代码:
# inX: 分类的输入向量
# dataSet: 输入的训练样本集
# labels: 标签向量
# k: 选择最近邻居的数目
def classify0(inX, dataSet, labels, k):
# 1.计算距离,这里采用的是欧式距离
dataSetSize = dataSet.shape[0] # 获取数据集大小,也就是有多少条数据
diffMat = tile(inX, (dataSetSize, 1)) - dataSet # 将待测试数据扩展
sqDiffMat = diffMat ** 2 # 差值矩阵中,矩阵元素分别平方
sqDistances = sqDiffMat.sum(axis = 1) # 横向求和,得到矩阵
distances = sqDistances ** 0.5 # 矩阵中,每个元素都开方
sortedDistIndicies = distances.argsort() # 距离排序
# 2.选择距离最小的k个点
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
# 3.排序
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=Ture)
return sortedClassCount[0][0]上述代码中有几点需要解释一下,也是我在学习的过程中查阅相关资料的地方。
第一,tile函数:
Numpy的 tile() 函数,就是将原矩阵横向、纵向地复制。
定义原矩阵:
>>> originMat = array([[1, 3], [2, 4]])横向:
>>> tile(originMat, 4) array([[1, 3, 1, 3, 1, 3, 1, 3], [2, 4, 2, 4, 2, 4, 2, 4]])纵向:
>>> tile(originMat, (3, 1)) array([[1, 3], [2, 4], [1, 3], [2, 4], [1, 3], [2, 4]])横向 + 纵向:
>>> tile(originMat, (3, 2)) array([[1, 3, 1, 3], [2, 4, 2, 4], [1, 3, 1, 3], [2, 4, 2, 4], [1, 3, 1, 3], [2, 4, 2, 4]])
第二,欧式距离,两个点的欧式距离公式如下:
$$
d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
第三,分组后的排序。将classCount字典分解为元组列表,然后使用程序第二行导入运算符模块的itemgetter方法,按照第二个元素的次序对元组进行排序 。此处的排序为逆序,即从大到小排序。
到现在为止,我们已经构造了第一个分类器,使用这个分类器可以完成很多分类任务。从这个实例出发,构造使用分类算法将会更加容易。
搞定!!!老板这次给我们加了一瓶可乐!!!有鸡腿有可乐!!!美滋滋!!!
我们在老板的安排下,已经使用k-近邻算法构造了第一个分类器,也可以检验分类器给出的答案是否符合我们的预期。
但是,分类器并不会得到百分百正确的结果,我们可以使用多种方法检测分类器的正确率。 此外分类器的性能也会受到多种因素的影响,如分类器设置和数据集等。不同的算法在不同数据集上的表现可能完全不同。
那么,问题来了,我们该如何测试分类器的效果呢?其中一种方法就是错误率。这是一种比较常用的评估方法,主要用于评估分类器在某个数据集上的执行效果。后面我们还会遇到更加适合的方法来测试分类器,但这里我们先只介绍错误率。
$$
错误率 = \frac {分类器给出错误结果的次数} {预测执行的总数}
$$
我们在已知答案的数据上进行测试,当然答案不能告诉分类器,检验分类器给出的结果是否符合预期结果。简单点说,我们用KNN训练出来了一个分类器,然后我们再把训练集丢到分类器里面,看看分类器的分类效果。
到现在,老板给出的任务我们也完成了,代码也写了一部分,也掌握了kNN算法的基本使用,还是很开心的!!
但是,老板又来了。
老板:小韩啊,你这个分类器倒是出来了,但是只在你自己捏造的数据集上运行,不行啊!!
我:(什么?敢说我的算法不行!!!)
老板:这样吧,明天我给你安排一个实在一点的任务,去改进一下约会网站的配对效果。
我:约会网站?听起来不错啊!那加鸡腿不?
老板:不加!!!
我: ̄へ ̄,老板,我先下班了,明天见!!!
最后,欢迎大家关注我的公众号,有什么问题也可以给我留言哦!

原文:https://www.cnblogs.com/xiaofeng-blog/p/10162173.html