Linear and Logistic Regression in TensorFlow

Graphs and sessions

TF Ops: constants, variables, functions

TensorBoard

Lazy loading

Linear Regression: Predict life expectancy from birth rate

Let‘s start with a simple linear regression example. I hope you all are already familiar with linear regression. If not, you can read about it on Wikipedia. Basically, we‘ll be building a very simple neural network consisting of one layer to infer the linear relationship between one explanatory variable X and one dependent variable Y.

Problem

I recently came across the visualization of the relationship between birth rates and life expectancies of different countries around the world and found that fascinating. Basically, it looks like the more children you have, the younger you are going to die! You can play the visualization created by Google based on the data collected by the World Bank here.

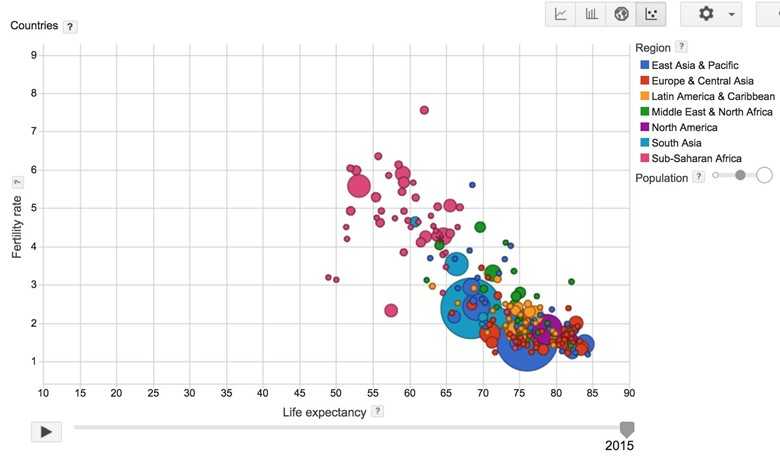
My question is, can we quantify that relationship? In other words, if the birth rate of a country is and its life expectancy is , can we find a linear function f such that ? If we know that relationship, given the birth rate of a country, we can predict the life expectancy of that country.

For this problem, we will be using a subset of the World Development Indicators dataset collected by the World Bank. For simplicity, we will be using data from the year 2010 only. You can download the data from class‘s GitHub folder here.

Dataset Description

Name: Birth rate - life expectancy in 2010

X = birth rate. Type: float.

Y = life expectancy. Type: foat.

Number of datapoints: 190

Approach

First, assume that the relationship between the birth rate and the life expectancy is linear, which means that we can find w and b such that .

To find w and b (in this case, they are both scalars), we will use backpropagation through a one layer neural network. For the loss function, we will be using mean squared error. After each epoch, we measure the mean squared difference between the actual value Ys and the predicted values of Ys.

You can download the file examples/03_linreg_starter.py from the class‘s GitHub repo to give it a shot yourself. After you‘re done, you can compare with the solution below. You can also visit examples/03_linreg_placeholder.py on GitHub for the executable script.

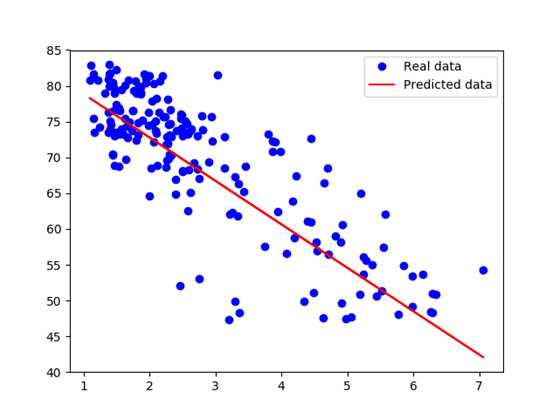
After training for 100 epochs, we got the average square loss to be 30.04 with w = -6.07, b = 84.93. It confirms our belief that there‘s a negative correlation between the birth rate and the life expectancy of a country. And no, it doesn‘t mean that having a child takes off 6 years of your life.

You can make other assumptions about the relationship between X and Y. For example, if we have a quadratic function:

To find w, u, and b for this model, we only have to add another variable u and change the formula for Y_predicted.

Control flow: Huber loss

Looking at the graph, we see that several outliers on the central bottom are outliers: they have low birth rate but also low life expectancy. Those outliers pull the fitted line towards them, making the model perform worse. One way to deal with outliers is to use Huber loss. Intuitively, squared loss has the disadvantage of giving too much weights to outliers (you square the difference - the larger the difference, the larger its square). Huber loss was designed to give less weight to outliers. Wikipedia has a pretty good article on it. Below is the Huber loss function:

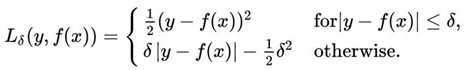
To implement this in TensorFlow, we might be tempted to use something Pythonic such as:

However, this approach would only work if TensorFlow‘s eager execution were enabled, which we will learn about in the next lecture. If we use the current version, TensorFlow would soon notify us that "TypeError: Using a `tf.Tensor` as a Python `bool` is not allowed." We will need to use control flow ops defined by TensorFlow. For the full list of those ops, please visit the official documentation.

To implement Huber loss, we can use either tf.greater, tf.less, or tf.cond. We will be using tf.cond since it‘s the most general. Other ops‘ usage is pretty similar.

This basically means that if the condition is true, use the true function. Else, use the false function.

With Huber loss, we found w: -5.883589, b: 85.124306. The graph compares the fitted line obtained by squared loss and Huber loss.

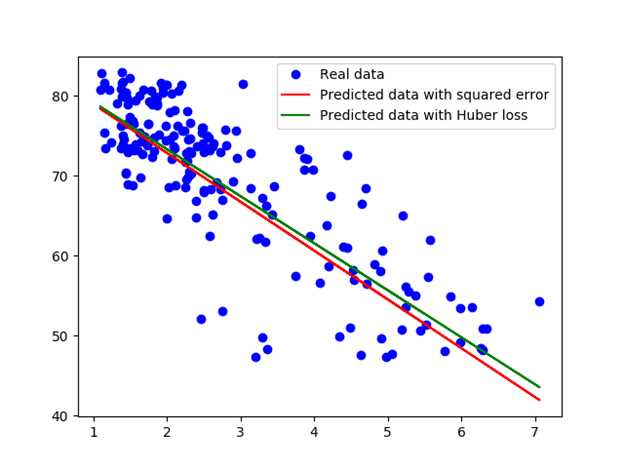
Which model performs better? Ah, we should have had a test set.

tf.data

You can visit examples/03_linreg_dataset.py on GitHub for the executable script.

According to Derek Murray in his introduction to tf.data, a nice thing about placeholder and feed_dicts is that they put the data processing outside TensorFlow, making it easy to shuffle, batch, and generate arbitrary data in Python. The drawback is that this mechanism can potentially slow down your program. Users often end up processing their data in a single thread and creating data bottleneck that slows execution down.

TensorFlow also offers queues as another option to handle your data. This provides performance as it lets you do pipelining, threading and reduces the time loading data into placeholders. However, queues are notorious for being difficult to use and prone to crashing.

Recently, demand for a better way to handle your data has been all the rage, and TensorFlow answers with tf.data module. It promises to be faster than placeholders and easier to use than queues, and doesn‘t crash. So how does this magical thing work?

Notice that in our linear regression, we stored the input data in a numpy array called data, each row of this numpy array is a pair value for (x, y), corresponding to a data point. To import this data into our TensorFlow model, we created placeholders for x (feature) and y (label). We then iterate through each data point with a for loop in step 8 and feed it into the placeholders with a feed_dict. We can, of course, use batches of data points instead of individual data points, but the key here is that the process of feeding the data from this numpy array to the TensorFlow model is slow and can get in the way of other execution of other ops.

With tf.data, instead of storing our input data in a non-TensorFlow object, we store it in a tf.data.Dataset object. We can create a Dataset from tensors with:

features and labels are supposed to be tensors, but remember that since TensorFlow and Numpy are seamlessly integrated, they can be NumPy arrays. We can initialize our dataset as followed:

Printing out type and shape of entries in the dataset for sanity check:

You can also create a tf.data.Dataset from files using one of TensorFlow‘s file format parsers, all of them have striking similarity to the old DataReader.

• tf.data.TextLineDataset(filenames): each of the line in those files will become one entry. It‘s good for datasets whose entries are delimited by newlines such as data used for machine translation or data in csv files.
• tf.data.FixedLengthRecordDataset(filenames): each of the data point in this dataset is of the same length. It‘s good for datasets whose entries are of a fixed length, such as CIFAR or ImageNet.
• tf.data.TFRecordDataset(filenames): it‘s good to use if your data is stored in tfrecord format.

Example:

After we have turned our data into a magical Dataset object, we can iterate through samples in this Dataset using an iterator. An iterator iterates through the Dataset and returns a new sample or batch each time we call get_next(). Let‘s start with make_one_shot_iterator(), we‘ll find out what it is in a bit. The iterator is of the class tf.data.Iterator.

Each time we execute ops X, Y, we get a new data point.

Now we can just compute Y_predicted and losses from X and Y just like you did with placeholders. The difference is that when you execute your graph, you no longer need to supplement data through feed_dict.

We have to catch the OutOfRangeError because miraculously, TensorFlow doesn‘t automatically catch it for us. If we run this code, we will see that we only get non zero loss in the first epoch. After that, the loss is always 0. It‘s because dataset.make_one_shot_iterator() literally gives you only one shot. It‘s fast to use -- you don‘t have to initialize it -- but it can be used only once. After one epoch, you reach the end of your data and you can‘t re-initialize it for the next epoch.

To use for multiple epochs, we use dataset.make_initializable_iterator(). At the beginning of each epoch, you have to re-initialize your iterator.

With tf.data.Dataset, you can batch, shuffle, repeat your data with just one command. You can also map each element of your dataset to transform it in a specific way to create a new dataset.

Does tf.data really perform better?

To compare the performance of tf.data with that of placeholders, I ran each model 100 times and calculated the average time each model took. On my Macbook Pro with 2.7 GHz Intel Core i5, the model with placeholder took on average 9.05271519 seconds, while the model with tf.data took on average 6.12285947 seconds. tf.data improves the performance by 32.4% compared to placeholders!

So yes, tf.data does deliver. It makes importing and processing data easier while making our program run faster.

Optimizers

In the code above, there are two lines that haven‘t been explained.

I remember the first time I ran into code similar to these, I was very confused.

• Why is optimizer in the fetches list of tf.Session.run()?
• How does TensorFlow know what variables to update?

optimizer is an op whose job is to minimize loss. To execute this op, we need to pass it into the list of fetches of tf.Session.run(). When TensorFlow executes optimizer, it will execute the part of the graph that this op depends on. In this case, we see that optimizer depends on loss, and loss depends on inputs X, Y, as well as two variables weights and bias.

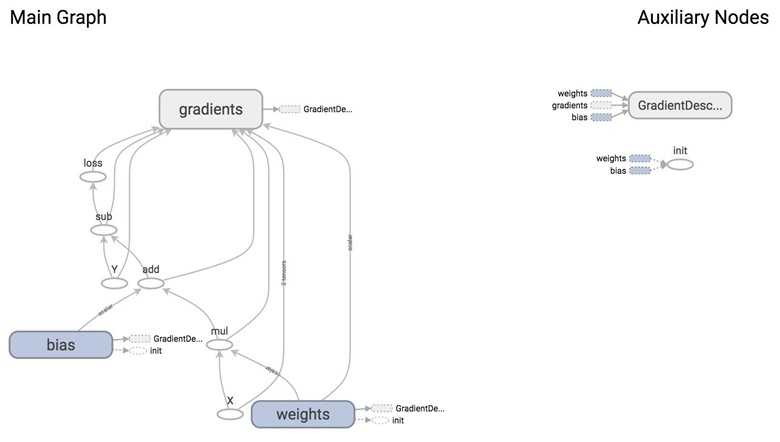
From the graph, you can see that the giant node GradientDescentOptimizer depends on 3 nodes: weights, bias, and gradients (which are automatically taken care of for us).

GradientDescentOptimizer means that our update rule is gradient descent. TensorFlow does auto differentiation for us, then update the values of w and b to minimize the loss. Autodiff is amazing!

By default, the optimizer trains all the trainable variables its objective function depends on. If there are variables that you do not want to train, you can set the keyword trainable=False when you declare a variable. One example of a variable you don‘t want to train is the variable global_step, a common variable you will see in many TensorFlow model to keep track of how many times you‘ve run your model.

You can also ask your optimizer to take gradients of specific variables. You can also modify the gradients calculated by your optimizer.

You can also prevent certain tensors from contributing to the calculation of the derivatives with respect to a specific loss with tf.stop_gradient.

This is very useful in situations when you want to freeze certain variables during training. Here are some examples given by TensorFlow‘s official documentation.

• When you train a GAN (Generative Adversarial Network) where no backprop should happen through the adversarial example generation process.
• The EM algorithm where the M-step should not involve backpropagation through the output of the E-step.

The optimizer classes automatically compute derivatives on your graph, but you can explicitly ask TensorFlow to calculate certain gradients with tf.gradients.

This method constructs symbolic partial derivatives of sum of ys w.r.t. x in xs. ys and xs are each a Tensor or a list of tensors. grad_ys is a list of Tensor, holding the gradients received by the ys. The list must be the same length as ys.

Technical detail: This is especially useful when training only parts of a model. For example, we can use tf.gradients() to take the derivative G of the loss w.r.t. to the middle layer. Then we use an optimizer to minimize the difference between the middle layer output M and M + G. This only updates the lower half of the network.

List of optimizers

GradientDescentOptimizer is not the only update rule that TensorFlow supports. Here is the list of optimizers that TensorFlow supports, as of 1/17/2017. The names are self-explanatory. You can visit the official documentation for more details:

tf.train.Optimizer

tf.train.GradientDescentOptimizer

tf.train.AdadeltaOptimizer

tf.train.AdagradOptimizer

tf.train.AdagradDAOptimizer

tf.train.MomentumOptimizer

tf.train.AdamOptimizer

tf.train.FtrlOptimizer

tf.train.ProximalGradientDescentOptimizer

tf.train.ProximalAdagradOptimizer

tf.train.RMSPropOptimizer

Sebastian Ruder, a PhD candidate at the Insight Research Centre for Data Analytics did a pretty great comparison of these optimizers in his blog post. If you‘re too lazy to read, here is the conclusion:

"RMSprop is an extension of Adagrad that deals with its radically diminishing learning rates. It is identical to Adadelta, except that Adadelta uses the RMS of parameter updates in the numerator update rule. Adam, finally, adds bias-correction and momentum to RMSprop. Insofar, RMSprop, Adadelta, and Adam are very similar algorithms that do well in similar circumstances. Kingma et al. [15] show that its bias-correction helps Adam slightly outperform RMSprop towards the end of optimization as gradients become sparser. Insofar, Adam might be the best overall choice."

TL;DR: Use AdamOptimizer.

Discussion questions

What are some of the real world problems that we can solve using linear regression? Can you write a quick program to do so?

Logistic Regression with MNIST

Let‘s build a logistic regression model in TensorFlow solving the good old classifier on the MNIST database.

The MNIST (Mixed National Institute of Standards and Technology database) is one of the most popular databases used for training various image processing systems. It is a database of handwritten digits. The images look like this:

Each image is 28 x 28 pixels. You can flatten each image to be a 1-d tensor of size 784. Each comes with a label from 0 to 9. For example, images on the first row is labelled as 0, the second as 1, and so on. The dataset is hosted on Yann Lecun‘s website.

TF Learn (the simplified interface of TensorFlow) has a script that lets you load the MNIST dataset from Yann Lecun‘s website and divide it into train set, validation set, and test set.

input_data.read_data_sets(‘data/mnist‘, one_hot=True) returns an instance of learn.datasets.base.Datasets, which contains three generators to 55,000 data points of training data (mnist.train), 10,000 points of test data (mnist.test), and 5,000 points of validation data (mnist.validation). You get the samples of these datasets by calling next_batch(batch_size), for example, mnist.train.next_batch(batch_size) with a batch_size of your choice. However, in real life, we often don‘t have access to an off the shelf data parser I thought it‘d be nice for us to just read in the MNIST data ourselves. It‘s also a good practice because in your real life work, you‘re likely to have to write your own data parser.

I‘ve already written the code for downloading and parsing MNIST data into numpy arrays in the file utils.py. All you need to do in your program is:

We choose flatten=True because we want each image to be flattened into a 1-d tensor. Each of train, val, and test in this case is a tuple of NumPy arrays, the first is a NumPy array of images, the second of labels. We need to create two Dataset objects, one for train set and one for test set (in this example, we won‘t be using val set).

The construction of the logistic regression model is pretty similar to the linear regression model. However, now we have A LOT more data. If we calculate gradient after every single data point it‘d be painfully slow. Fortunately, we can process the data in batches.

The next step is to create an iterator to get samples from the two datasets. In the linear regression example, we used only the train set, so it was okay to create an iterator for that dataset and just draw samples from that dataset. When we have more than one dataset, if we have one iterator for each dataset, we would need to build one graph for each iterator! A better way to do it is to create one single iterator and initialize it with a dataset when we need to draw data from that dataset.

Similar to linear regression, you can download the starter file examples/03_logreg_starter.py from the class‘s GitHub repo and give it a shot. You can see the solution at examples/03_logreg.py.

Running on my Mac, the batch version of the model with batch size 128 runs in 1 second, while the non-batch model runs in 30 seconds! Note that larger batch size typically requires more epochs since it does fewer update steps. See "mini-batch size" in Bengio‘s practical tips. Larger batch size also requires more memory.

We achieved the accuracy of 91.34% after 30 epochs. This is about as good as we can get from a linear classifier.

Shuffling can affect performance: without shuffling, the accuracy is consistently at 91.34%. With shuffle, the accuracy fluctuates between 88% to 93%.

Let‘s see what our graph looks like on TensorBoard.

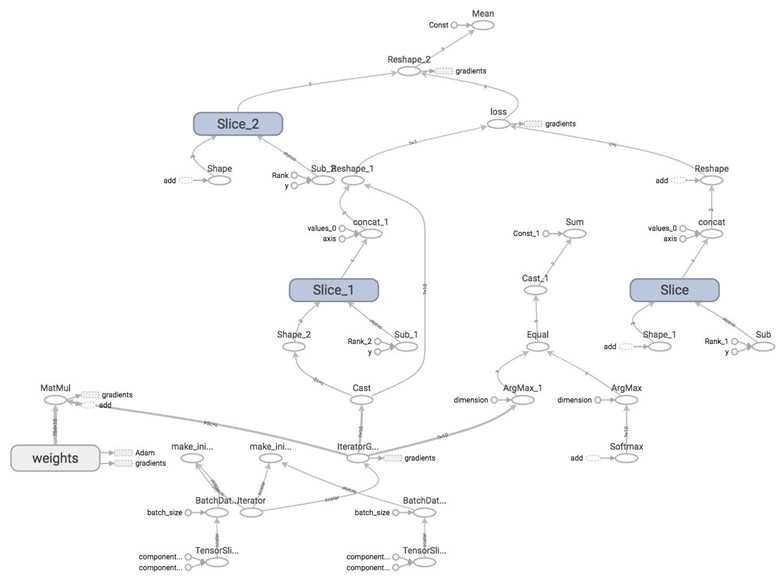
WOW

I know. That‘s why we‘ll learn how to structure our model in the next lecture!

Linear and Logistic Regression in TensorFlow

原文：https://www.cnblogs.com/kexinxin/p/10162824.html