最近浅学了一下匈牙利算法,略有感触,发文记录一下
匈牙利算法是用在二分图匹配中的
所以要先知道二分图的几个概念
二分图:
把一个图的顶点划分为两个不相交的集合 U 和 V ,且使得每一条边都分别连接 U 、V 中的顶点,如果存在这样的划分,则称此图为二分图。
简单说,就是可以把一个图分为两部分,同一部分里没有边相连
匹配:
二分图匹配就是边集中的任意两条边没有公共顶点
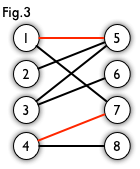
如图,图中的红边叫做匹配
最大匹配:
一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配
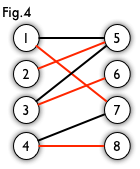
当然,最大匹配不一定只存在一种
完美匹配
如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配
上图就是一个完美匹配,完美匹配一定是最大匹配,完美匹配也可能存在多种,但并不是所有的图都有完美匹配
然后开始我们的匈牙利算法
接着是关于它的两个概念
交替路
从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边······形成的路径叫交替路。
增广路:
从一个未匹配的点出发,走交替路,如果路过一个未匹配的点,这条交替路叫增广路
关于匹配的概念就这些,这是在做题过程中可能会遇到的东西
顶点覆盖:
在顶点集合中,选取一部分顶点,这些顶点能够把所有的边都覆盖了。这些点就是顶点覆盖集
最小顶点覆盖:
在所有的顶点覆盖集中,顶点数最小的那个叫最小顶点集合。
独立集:
在所有的顶点中选取一些顶点,这些顶点两两之间没有连线,这些点就叫独立集
最大独立集:
在左右的独立集中,顶点数最多的那个集合
路径覆盖:
在图中找一些路径,这些路径覆盖图中所有的顶点,每个顶点都只与一条路径相关联。
最小路径覆盖:
在所有的路径覆盖中,路径个数最小的就是最小路径覆盖了。
原文:https://www.cnblogs.com/lykkk/p/10164171.html