算法第五章 | 回溯算法
一、 回溯算法
回溯法有“通用的解题法”之称。可以系统地搜索一个问题的所有解或任一解,是一个既带有系统性又带有跳跃性的搜索算法。
它在问题的解空间树中,按深度优先策略,从根节点出发搜索解空间树。算法搜索至解空间树的任一结点时,先判断该结点是否包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的搜索,逐层向其祖先结点回溯。否则,进入该子树,继续按深度优先策略搜索。回溯法求问题的所有解时,要回溯到根,且根结点的所有子树都已被搜索遍才结束。回溯法求问题的一个解时,只要搜索到问题的一个解就可结束。
这种以深度优先方式系统搜索问题的解的搜索问题解的算法称为回溯法,它适用于组合数较大的问题。
1.问题的解空间
用回溯法解问题时,应明确定义问题的解空间,问题的解空间至少应包含问题的一个(最优)解。
定义了问题的解空间后,还应将解空间很好地组织起来,使得能用回溯法方便地搜索整个解空间。通常将解空间组织成树或图的形式。
例:n=3时的0-1背包问题,可用一棵完全二叉树表示其解空间。
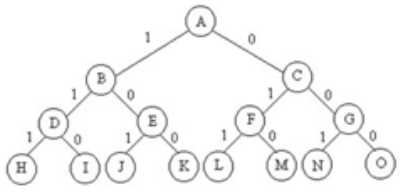
(图) 0-1背包的解空间树
2.回溯法的基本思想
确定了解空间的组织结构后,回溯法从开始结点(根结点)出发,以深度优先方式搜索整个解空间。这个开始结点成为活结点,同时也成为当前的扩展结点。在当前的扩展结点处,搜索向纵深方向移至一个新节点。该新节点成为新的活结点,并成为当前扩展结点。如果在当前的扩展结点出不能再向纵深方向移动,则当前扩展就成为死结点。此时,应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点。回溯法以这种工作方式递归地在解空间中搜索,直至找到所要求的解或解空间中已无活点为止。
3.约束函数
回溯法搜索解空间时,通常采用两种策略避免无效搜索,提高回溯法的搜索效率。
其一是用约束函数在扩展结点处剪去不满足约束的子树。
其二是用限界函数剪去得不到最优解的子树。
这两类函数统称为剪枝函数。
二、 “子集和”问题的解空间结构和约束函数
1.问题描述:设集合S={x1,x2,…,xn}是一个正整数集合,c是一个正整数,子集和问题判定是否存在S的一个子集S1,使S1中的元素之和为c。试设计一个解子集和问题的回溯法。
2.解空间结构:
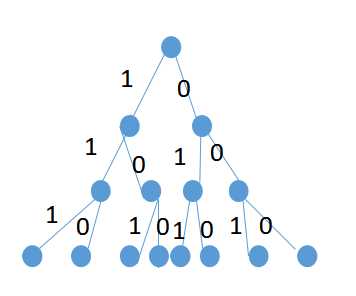
(图)解空间结构
3.约束函数:
If (c < sum) {v[p] = false; sum-= data[p];}
4.具体代码如下:
bool traceback(int n) {
int p = 0, sum = 0;
while (p >= 0) {
if (!v[p]) {
v[p] = true;
sum += data[p];
if (c == sum)
return true;
else if (c < sum) {
v[p] = false;
sum -= data[p];
}
p++;
}
if (p >= n) {
while (v[p - 1]) {
p--;
v[p] = false;
if (p<1) return false;
}
while (!v[p - 1]) {
p--;
if (p<1) return false;
}
sum -= data[p - 1];
v[p - 1] = false;
}
}
return false;
}
三、 学习过程中遇到的问题及结对编程情况
1.实现回溯算法的能力有待提高。
2.未能熟练掌握套子集数模板的能力。
3.与队友交流过模板及剪枝的问题。
原文:https://www.cnblogs.com/ljl-gd/p/10137145.html