参考:https://blog.csdn.net/zengxiantao1994/article/details/70210662
Matlab代码:
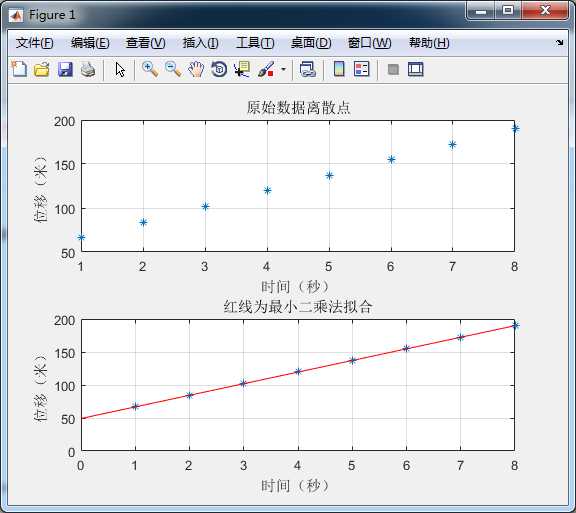
N = 8; x = [1 2 3 4 5 6 7 8 ]; y = [67 84 102 120 137 155 172 190]; subplot(2,1,1); plot(x,y,‘*‘); % 图形的一些设置 xlabel(‘时间(秒)‘); ylabel(‘位移(米)‘); title(‘原始数据离散点‘) grid on subplot(2,1,2); p = polyfit(x,y,1); %得出P就是线性拟合的系数 % 0:0.01:9 x1 = 0:1:N; %起始为0,终点为N,步长1 y1 = polyval(p,x1); plot(x,y,‘*‘,x1,y1,‘r‘) xlabel(‘时间(秒)‘); ylabel(‘位移(米)‘); title(‘红线为最小二乘法拟合‘) grid on sumxyji =sum(x.*y); %向量内积 sumx = sum(x); sumy = sum(y); sumxx = sum(x.*x); k = (N*sumxyji - sumx*sumy)/(N*sumxx-sumx*sumx) b = (sumy-k*sumx)/N
效果:
自己C语言实现:
公式:
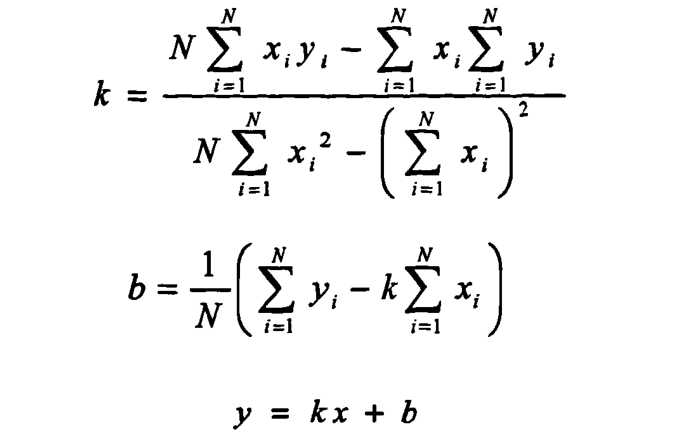
#include <stdio.h> #include <stdlib.h> //函数功能:进行最小二乘曲线拟合(拟合y=a0+a1*x),计算出对应的系数a //参数说明: // n: 给定数据点的个数 // x[]: 存放给定n个数据点的X坐标 // y[]: 存放给定n个数据点的Y坐标 // k,b: 拟合多项式的系数,表示多项式的k,b void polyfit(int n,double x[],double y[],double &k,double &b) { int i,j; double sumxymultiply = 0.0; double sumx = 0.0; double sumy = 0.0; double sumxx = 0.0; for (i=0;i<n;i++) { sumx += x[i]; sumy += y[i]; sumxymultiply += (x[i]*y[i]); sumxx += (x[i]*x[i]); } k = (n*sumxymultiply - sumx*sumy)/(n*sumxx - sumx*sumx); b = (sumy-k*sumx)/n; } void printArr(double *arr,int n) { for(int i=0;i<n;++i) printf("%lf ",arr[i]); printf("\n"); } int main() { const int N = 8; double x[N] = {1,2,3, 4,5,6,7,8}; double y[N] = {67,84,102,120,137,155,172,190}; double k,b; polyfit(N,x,y,k,b); printf("%lf %lf\n",k,b); return 0; }
原文:https://www.cnblogs.com/shuqingstudy/p/10164469.html