繁琐细节题。
1、线段无交点时,ans=0;
2、如图 假设过p3.y的水平线与p1p2相交
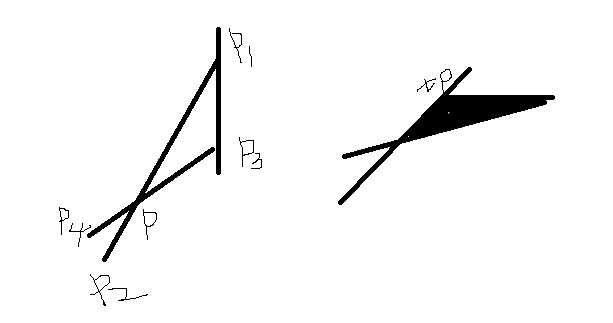
因为雨是垂直下落的,左图的情况是无法收集到雨水的

1 #include <iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<stdlib.h> 6 #include<vector> 7 #include<cmath> 8 #include<queue> 9 #include<set> 10 using namespace std; 11 #define N 100000 12 #define LL long long 13 #define INF 0xfffffff 14 const double eps = 1e-8; 15 const double pi = acos(-1.0); 16 const double inf = ~0u>>2; 17 struct point 18 { 19 double x,y; 20 point(double x=0,double y=0):x(x),y(y) {} 21 } p[10]; 22 typedef point pointt; 23 pointt operator -(point a,point b) 24 { 25 return pointt(a.x-b.x,a.y-b.y); 26 } 27 int dcmp(double x) 28 { 29 if(fabs(x)<eps) return 0; 30 return x<0?-1:1; 31 } 32 double cross(point a,point b) 33 { 34 return a.x*b.y-a.y*b.x; 35 } 36 bool cmp(point a,point b) 37 { 38 return a.y>b.y; 39 } 40 41 bool intersection1(point p1, point p2, point p3, point p4, point& p) // 直线相交 42 { 43 double a1, b1, c1, a2, b2, c2, d; 44 a1 = p1.y - p2.y; 45 b1 = p2.x - p1.x; 46 c1 = p1.x*p2.y - p2.x*p1.y; 47 a2 = p3.y - p4.y; 48 b2 = p4.x - p3.x; 49 c2 = p3.x*p4.y - p4.x*p3.y; 50 d = a1*b2 - a2*b1; 51 if (!dcmp(d)) return false; 52 p.x = (-c1*b2 + c2*b1) / d; 53 p.y = (-a1*c2 + a2*c1) / d; 54 return true; 55 } 56 double solve(point p1,point p2,point p3,point p4,point pp,point tp) 57 { 58 double ans; 59 point p11 = point(p1.x,p1.y+1); 60 if(dcmp(cross(p11-p1,p1-p3))==0) 61 { 62 ans = 0; 63 //cout<<","; 64 } 65 else 66 { 67 if(dcmp(cross(p11-p1,p1-p3))*dcmp(cross(p1-p2,p3-p4))<0) 68 { 69 ans = fabs(cross(p3-pp,tp-pp))/2; 70 //cout<<","; 71 } 72 else ans = 0; 73 } 74 return ans; 75 } 76 int on_segment( point p1,point p2 ,point p ) 77 { 78 double max=p1.x > p2.x ? p1.x : p2.x ; 79 double min =p1.x < p2.x ? p1.x : p2.x ; 80 double max1=p1.y > p2.y ? p1.y : p2.y ; 81 double min1=p1.y < p2.y ? p1.y : p2.y ; 82 if( p.x >=min && p.x <=max && 83 p.y >=min1 && p.y <=max1 ) 84 return 1; 85 else 86 return 0; 87 } 88 int main() 89 { 90 int t,i; 91 cin>>t; 92 while(t--) 93 { 94 for(i = 1; i <= 4 ; i++) 95 scanf("%lf%lf",&p[i].x,&p[i].y); 96 sort(p+1,p+3,cmp); 97 sort(p+3,p+5,cmp); 98 point pp; 99 if(intersection1(p[1],p[2],p[3],p[4],pp)) 100 { 101 if(!on_segment(p[1],p[2],pp)||!on_segment(p[3],p[4],pp)) 102 { 103 puts("0.00"); 104 continue; 105 } 106 } 107 //cout<<pp.x<<" "<<pp.y<<endl; 108 double ans; 109 point p1 = point(p[3].x-1,p[3].y),p2; 110 point p3 = point(p[1].x-1,p[1].y); 111 if(intersection1(p[1],p[2],p[3],p1,p2)&&on_segment(p[1],p[2],p2)) 112 { 113 114 ans = solve(p[1],p[2],p[3],p[4],pp,p2); 115 } 116 else 117 { 118 intersection1(p[3],p[4],p[1],p3,p2); 119 // cout<<p2.x<<" "<<p2.y<<endl; 120 ans = solve(p[3],p[4],p[1],p[2],pp,p2); 121 } 122 printf("%.2f\n",ans+eps); 123 124 } 125 return 0; 126 }
poj2826An Easy Problem?!,布布扣,bubuko.com
原文:http://www.cnblogs.com/shangyu/p/3885912.html