一张手写的题解
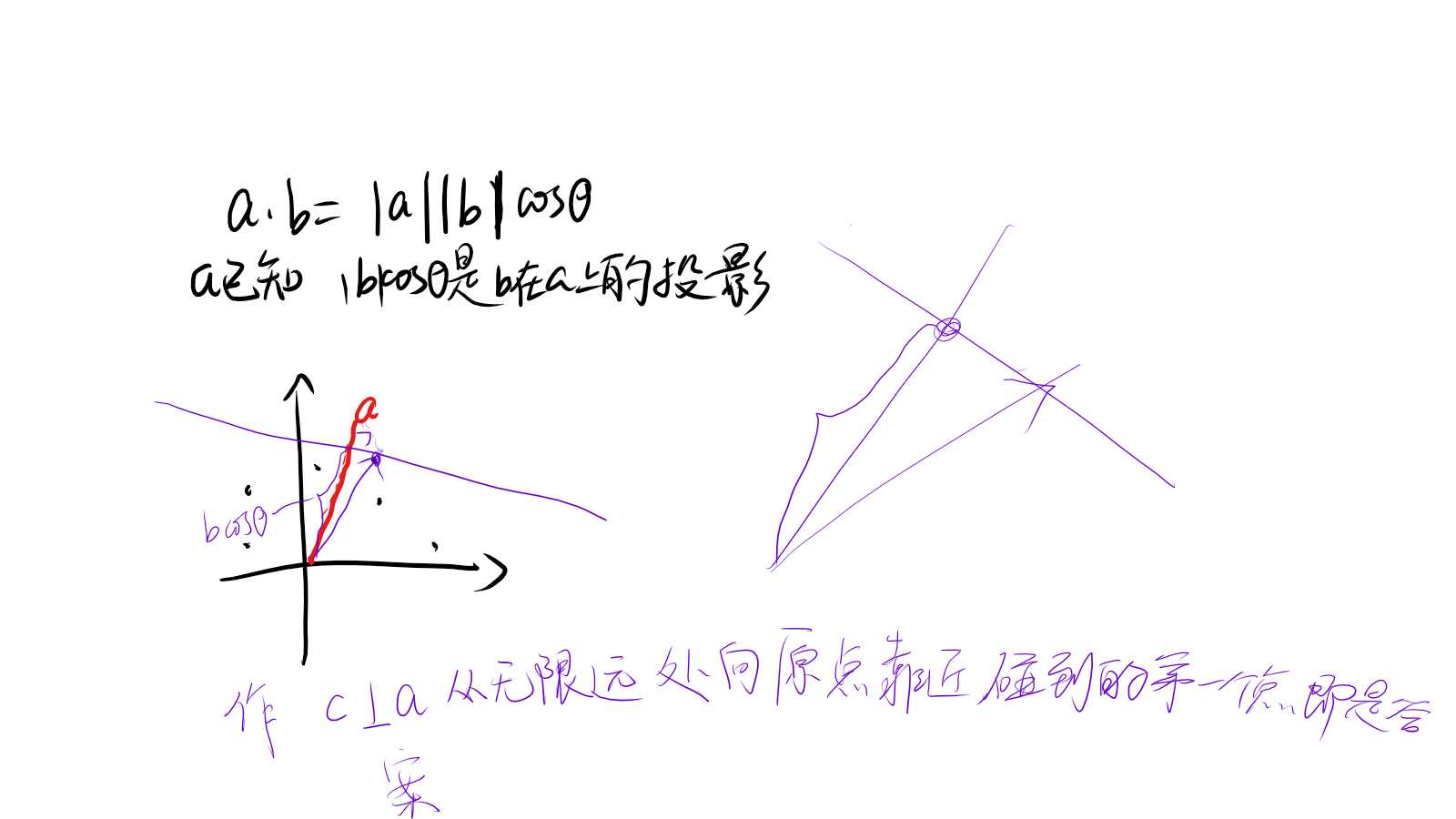
这些点一定在凸壳上
证明可以参照gxz大佬的题解
这个题的做法是按照询问作为时间轴,把每个插入的向量视为在一个时间区间 \([l,r]\) 内有效,在 \([l,r]\) 在线段树上对应的 \(O(log n)\) 个区间上打上标记,然后dfs一下整棵线段树,对于每个dfs到的线段树节点,遍历这个节点有的标记,维护出凸壳,然后在凸壳上二分斜率(也可以三分~),更新这个节点对应区间的询问的答案(这样不需要进行删除操作)
对着std调了好久...
每次二分是 \(O(logn)\) 每个节点被插入了 \(O(logn)\) 次,总共插入了 \(O(nlogn)\)次,所以复杂度是 \(O(nlog^2n)\)
好像有个什么性质可以少个log,但这份代码居然跑进了前两页,所以似乎没必要了,其实是不想再写了
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 7;
typedef long long ll;
typedef long double lf;
const lf eps = 1e-8;
template<class A, class B> inline void chmax(A &a, B b) {
if (a < b) a = b;
}
inline int read() {
register int c = getchar(), x = 0;
while (!isdigit(c)) c = getchar();
while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
return x;
}
struct Vec {
int x, y;
Vec(int x, int y) : x(x), y(y) {}
Vec() {}
inline Vec operator +(const Vec&b) const {return Vec(x + b.x, y + b.y);}
inline Vec operator -(const Vec&b) const {return Vec(x - b.x, y - b.y);}
inline ll operator *(const Vec&a) const {return x * 1ll * a.x + y * 1ll * a.y;}
inline ll operator %(const Vec&a) const {return x * 1ll * a.y - y * 1ll * a.x;}
} q[MAXN];
struct atom {
Vec a, b;//b是有效时间
} a[MAXN];
int n, op, x, y, sta[MAXN], top, tot, tot1; //因为栈存的是编号,所以数组嵌套有点多,可以存vec减少嵌套
ll ans[MAXN];
vector<int> t[530000];
inline bool cmp(int x, int y) {
if (a[x].a.x != a[y].a.x) return a[x].a.x < a[y].a.x;//按照x,y排序 求出凸壳
return a[x].a.y < a[y].a.y;
}
inline void add(int o, int l, int r, int ql, int qr, int v) {
if (ql > qr) return ;
if (ql <= l && r <= qr) return void(t[o].push_back(v));
int mid = l + r >> 1;
if (ql <= mid) add(o << 1, l, mid, ql, qr, v);
if (qr > mid) add(o << 1 | 1, mid + 1, r, ql, qr, v);
}
inline lf slope(const Vec &a, const Vec &b) {
if (fabs(a.x - b.x) < eps) return 1e9;
return lf(a.y - b.y) / (a.x - b.x);
}
inline ll query(int o, int pos) { //二分q[pos]垂线的斜率处于凸包的哪个位置
lf K = -1.0 * q[pos].x / q[pos].y;
//-1.0 / (q[pos].y / q[pos].x);
if (top == 1 || K > slope(a[t[o][sta[1]]].a, a[t[o][sta[2]]].a) + eps) return q[pos] * a[t[o][sta[1]]].a;
if (K + eps < slope(a[t[o][sta[top - 1]]].a, a[t[o][sta[top]]].a)) return q[pos] * a[t[o][sta[top]]].a;//判边界,不知道哪些不需要...但判了总没坏处
int l = 2, r = top, ans = 1;
while (l <= r) {
int mid = l + r >> 1;
if (K < slope(a[t[o][sta[mid - 1]]].a, a[t[o][sta[mid]]].a) + eps) ans = mid, l = mid + 1;
else r = mid - 1;
}
return q[pos] * a[t[o][sta[ans]]].a;
}
inline void solve(int o, int l, int r) {
if (!t[o].size()) return ;
sort(t[o].begin(), t[o].end(), cmp);
top = 0;
for (int i = 0; i < t[o].size(); ++i) {
while (top > 1 && (a[t[o][i]].a - a[t[o][sta[top - 1]]].a) % (a[t[o][sta[top]]].a - a[t[o][sta[top - 1]]].a) <= 0) --top;//维护凸壳
sta[++top] = i;
}
for (int i = l; i <= r; ++i) chmax(ans[i], query(o, i));
}
inline void dfs(int o, int l, int r) {
solve(o, l, r);
if (l == r) return ;
int mid = l + r >> 1;
dfs(o << 1, l, mid), dfs(o << 1 | 1, mid + 1, r);
}
int main() {
int m = read();
while (m--) {
op = read(), x = read();
if (op != 2) {
y = read();
if (op == 1) a[++tot1] = (atom) {Vec(x, y), Vec(tot + 1, -1)};
else q[++tot] = Vec(x, y);
}
else a[x].b.y = tot;
}
for (int i = 1; i <= tot1; ++i) add(1, 1, tot, a[i].b.x, a[i].b.y == -1 ? tot : a[i].b.y, i);
dfs(1, 1, tot);
for (int i = 1; i <= tot; ++i) printf("%lld\n", ans[i]);
return 0;
}[BZOJ4311]向量[线段树分治+计算几何+二分/三分]
原文:https://www.cnblogs.com/storz/p/10192431.html