第一类:
S(n,m)表示把n个元素组合成m个圆排列的方案数(注意是圆排列,n个元素的圆排列方案数:n!/n=(n-1)!)
递推式:
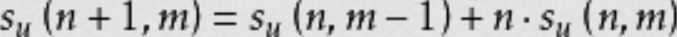
考虑最后一个放在哪里。
性质:

例题:HDU 4372 Count the Buildings——第一类斯特林数
第二类:
s(n,m)表示把n个不同元素放进m个相同盒子的方案数(m个集合)
还是考虑最后一个放在哪里
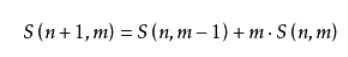

第二类斯特林数组合意义比较强大(毕竟没有排列苛刻的限制嘛)
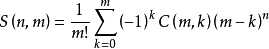
证明考虑容斥,枚举哪些个盒子一定不放球,其他爱放不放(Venn图)
原文:https://www.cnblogs.com/Miracevin/p/10193387.html