lrb有一棵树,树的每个节点有个颜色。给一个长度为n的颜色序列,定义s(i,j) 为i 到j 的颜色数量。以及
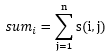
现在他想让你求出所有的sum[i]
输入格式:
第一行为一个整数n,表示树节点的数量
第二行为n个整数,分别表示n个节点的颜色c[1],c[2]……c[n]
接下来n-1行,每行为两个整数x,y,表示x和y之间有一条边
输出格式:
输出n行,第i行为sum[i]
输入样例#1:
5
1 2 3 2 3
1 2
2 3
2 4
1 5输出样例#1:
10
9
11
9
12链上信息,可以考虑点分治。
那么问题就转化为了:如何在\(O(n)\)的时间内求出经过\(rt\)的所有链信息,并把答案更新到每个点上。
这样显然不是很好做,考虑算每种颜色的贡献。
对于一种颜色,只有他第一次出现的时候才会造成一点贡献,可以考虑记个桶来维护颜色的贡献。
具体的,对于当前的分治块,对\(rt\)的每个儿子的子树\(dfs\),如果当前点的颜色是\(rt\)到当前点这条链上第一次出现,那么就把当前点的\(size\)加入桶。
先把所有儿子的子树全处理完,弄出来一个桶,注意根的颜色特判。
然后统计答案,枚举根的儿子,先消除当前子树对桶的贡献,然后对当前子树\(dfs\),若当前点颜色第一次出现,就把当前颜色的桶的值改为\(sz[rt]-sz[x]\),\(x\)为当前儿子。
然后记得回溯时还原,每个子树统计完答案把影响加回来,更改桶的时候同时维护一个\(sum\)。
细节挺多的,具体看代码。
#include<bits/stdc++.h>
using namespace std;
#define int long long //偷下懒QAQ
void read(int &x) {
x=0;int f=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-f;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';x*=f;
}
void print(int x) {
if(!x) return ;if(x<0) x=-x,putchar('-');
print(x/10),putchar(x%10+48);
}
void write(int x) {if(!x) putchar('0');else print(x);puts("");}
const int maxn = 1e5+10;
const int mod = 1e9+7;
int n,m,col[maxn];
struct Input_Tree {
int head[maxn],tot,vis[maxn],sz[maxn],f[maxn],rt,t[maxn],ans[maxn],size,siz[maxn],r[maxn],sum,del_sz;
struct edge{int to,nxt;}e[maxn<<1];
void add(int u,int v) {e[++tot]=(edge){v,head[u]},head[u]=tot;}
void ins(int u,int v) {add(u,v),add(v,u);}
void get_rt(int x,int fa) {
sz[x]=1,f[x]=0;
for(int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to]&&e[i].to!=fa) {
get_rt(e[i].to,x);sz[x]+=sz[e[i].to];
f[x]=max(f[x],sz[e[i].to]);
}
f[x]=max(f[x],size-sz[x]);
if(f[x]<f[rt]) rt=x;
}
void get_t(int x,int fa,int delta) {
sz[x]=1;r[col[x]]++;
for(int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to]&&e[i].to!=fa)
get_t(e[i].to,x,delta),sz[x]+=sz[e[i].to];
r[col[x]]--;
if(!r[col[x]]&&col[x]!=col[rt]) t[col[x]]+=sz[x]*delta,sum+=sz[x]*delta;
}
void get_ans(int x,int fa) {
int tmp=t[col[x]];
if(!r[col[x]]&&col[x]!=col[rt]) t[col[x]]=del_sz,sum=sum-tmp+del_sz;
ans[x]+=sum;
r[col[x]]++;
for(int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to]&&e[i].to!=fa) get_ans(e[i].to,x);
r[col[x]]--;
if(!r[col[x]]&&col[x]!=col[rt]) sum=sum-t[col[x]]+tmp,t[col[x]]=tmp;
}
void clear(int x,int fa) {
t[col[x]]=r[col[x]]=0;
for(int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to]&&e[i].to!=fa) clear(e[i].to,x);
}
void solve(int x) {
vis[x]=1;
clear(x,0);sum=0;
for(int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to]) get_t(e[i].to,x,1);
del_sz=1;
for(int i=head[x];i;i=e[i].nxt) if(!vis[e[i].to]) del_sz+=sz[e[i].to];
t[col[x]]=del_sz;sum+=del_sz;
ans[x]+=sum;
for(int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to]) {
get_t(e[i].to,x,-1);del_sz-=sz[e[i].to];
t[col[x]]-=sz[e[i].to],sum-=sz[e[i].to];
get_ans(e[i].to,x);
get_t(e[i].to,x,1);del_sz+=sz[e[i].to];
t[col[x]]+=sz[e[i].to],sum+=sz[e[i].to];
}
for(int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to]) size=sz[e[i].to],rt=0,get_rt(e[i].to,x),solve(rt);
}
void work() {
size=n,f[0]=maxn,get_rt(1,0);
solve(rt);for(int i=1;i<=n;i++) write(ans[i]);
}
}T;
signed main() {
read(n);
for(int i=1;i<=n;i++) read(col[i]);
for(int i=1,x,y;i<n;i++) read(x),read(y),T.ins(x,y);
T.work();
return 0;
}原文:https://www.cnblogs.com/hbyer/p/10257773.html