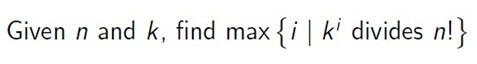
2 2 2 10 10
Case 1: 1 Case 2: 2
给定n和k, 求 n! 能被 k^i 整除时,i 的最大取值。
解题思路:
将k分解质因素,问题变为,(1×2×3×...×n) 要被 ( p1^(i*a1) × p2^(i*a2) × ... × pn^(i*an) ) 整除,即分子中各分母的质因数的幂次要大于等于分母。
所以根据k的各质因素,求出满足各质因数的幂次 分子>=分母 的关系限制i,算出最大的i即可。
这题要用到unsigned long long,比较坑。。
参考代码:
#include <iostream>
#include <cstring>
#include <cmath>
#define INF 9223372036854775807ULL
using namespace std;
typedef unsigned long long ull;
const int MAXN = 10000010;
int T, cnt;
ull N, K, ans, factorA[MAXN], factorB[MAXN], totFactor, prime[MAXN], totPrime;
bool isPrime[MAXN];
void getPrime(ull n) {
memset(isPrime, true, sizeof(isPrime));
totPrime = 0;
for (ull i = 2; i <= n; i++) {
if (isPrime[i]) {
prime[++totPrime] = i;
}
for (ull j = 1; j <= totPrime && i*prime[j] <= n; j++) {
isPrime[i*prime[j]] = false;
if (i % prime[j] == 0) break;
}
}
}
void getFactor(ull n) {
/*
ull now = n;
totFactor = 0;
for (ull i = 2; i*i <= n; i++) {
if (now % i == 0) {
factorA[++totFactor] = i;
factorB[totFactor] = 0;
while (now % i == 0) {
factorB[totFactor]++;
now /= i;
}
}
}
if (now != 1) {
factorA[++totFactor] = now;
factorB[totFactor] = 1;
}
*/
totFactor = 0;
ull now = n;
for (ull i = 1; i <= totPrime && prime[i] <= now; i++) {
if (now % prime[i] == 0) {
factorA[++totFactor] = prime[i];
factorB[totFactor] = 0;
while (now % prime[i] == 0) {
factorB[totFactor]++;
now /= prime[i];
}
}
}
if (now != 1) {
factorA[++totFactor] = now;
factorB[totFactor] = 1;
}
}
void solve() {
if (K == 1) {
cout << "Case " << ++cnt << ": inf" << endl;
} else {
getFactor(K);
ans = INF;
for (ull i = 1; i <= totFactor; i++) {
ull temp = N, sum = 0;
while (temp > 0) {
sum += temp / factorA[i];
temp /= factorA[i];
}
if (sum / factorB[i] < ans) {
ans = sum / factorB[i];
}
}
cout << "Case " << ++cnt << ": " << ans << endl;
}
}
int main() {
ios::sync_with_stdio(false);
cin >> T;
getPrime(10000000);
while (T--) {
cin >> N >> K;
solve();
}
return 0;
}HDU 3988 Harry Potter and the Hide Story(数论-整数和素数),布布扣,bubuko.com
HDU 3988 Harry Potter and the Hide Story(数论-整数和素数)
原文:http://blog.csdn.net/wujysh/article/details/38358555