我们知道,通过对数组进行直接寻址(Direct Addressing),可以在 O(1) 时间内访问数组中的任意元素。所以,如果存储空间允许,可以提供一个数组,为每个可能的关键字保留一个位置,就可以应用直接寻址技术。
哈希表(Hash Table)是普通数组概念的推广。当实际存储的的关键字数比可能的关键字总数较小时,这时采用哈希表就会比使用直接数组寻址更为有效。因为哈希表通常采用的数组尺寸与所要存储的关键字数是成比例的。
哈希表是一种动态集合数据结构,在一些合理的假设下,在哈希表中查找一个元素的期望时间是 O(1) 。
现在假设我们要使用员工的社保号作为唯一标识进行存储。社保号的格式为 DDD-DD-DDDD(D 的范围为数字 0-9)。
如果使用 Array 存储员工信息,要查询社保号为 111-22-3333 的员工,则将会尝试遍历数组的所有位置,即执行渐进时间为 O(n) 的查询操作。好一些的办法是将社保号排序,以使查询渐进时间降低到 O(log(n))。但理想情况下,我们更希望查询渐进时间为 O(1)。
一种方案是建立一个大数组,范围从 000-00-0000 到 999-99-9999 。
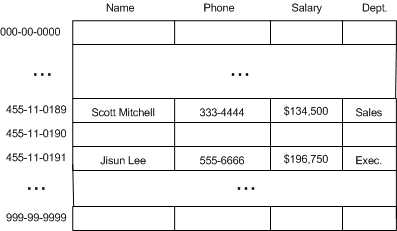
这种方案的缺点是浪费空间。如果我们仅需要存储 1000 个员工的信息,那么仅利用了 0.0001% 的空间。
第二种方案就是用哈希函数(Hash Function)压缩序列。
我们选择使用社保号的后四位作为索引,以减少区间的跨度。这样范围将从 0000 到 9999。
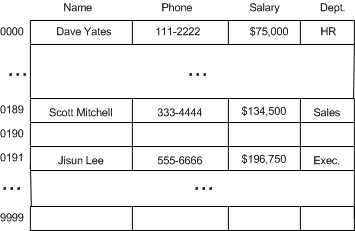
在数学上,将这种从 9 位数转换为 4 位数的方式称为哈希转换(Hashing)。可以将一个数组的索引空间(indexers space)压缩至相应的哈希表(Hash Table)。
在上面的例子中,哈希函数的输入为 9 位数的社保号,输出结果为后 4 位。
H(x) = last four digits of x
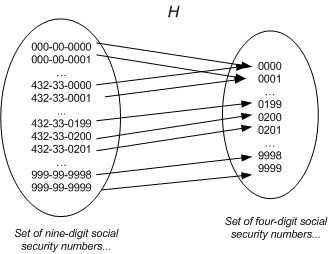
上图中也说明在哈希函数计算中常见的一种行为:哈希冲突(Hash Collisions)。即有可能两个社保号的后 4 位均为 0000。
当要添加新元素到 Hashtable 中时,哈希冲突是导致操作被破坏的一个因素。如果没有冲突发生,则元素被成功插入。如果发生了冲突,则需要判断冲突的原因。因此,哈希冲突提高了操作的代价,Hashtable 的设计目标就是要尽可能减低冲突的发生。
处理哈希冲突的方式有两种:避免和解决,即冲突避免机制(Collision Avoidance)和冲突解决机制(Collision Resolution)。
避免哈希冲突的一个方法就是选择合适的哈希函数。哈希函数中的冲突发生的几率与数据的分布有关。例如,如果社保号的后 4 位是随即分布的,则使用后 4 位数字比较合适。但如果后 4 位是以员工的出生年份来分配的,则显然出生年份不是均匀分布的,则选择后 4 位会造成大量的冲突。我们将这种选择合适的哈希函数的方法称为冲突避免机制(Collision Avoidance)。
在处理冲突时,有很多策略可以实施,这些策略称为冲突解决机制(Collision Resolution)。其中一种方法就是将要插入的元素放到另外一个块空间中,因为相同的哈希位置已经被占用。
哈希冲突解决策略:开放寻址法(Open Addressing)
通常采用的冲突解决策略为开放寻址法(Open Addressing),将所有的元素都存放在哈希表内的数组中,不使用额外的数据结构。
开放寻址法的最简单的一种实现就是线性探查(Linear Probing),步骤如下:
现在如果我们要将五个员工的信息插入到哈希表中:
则插入后的哈希表可能如下:
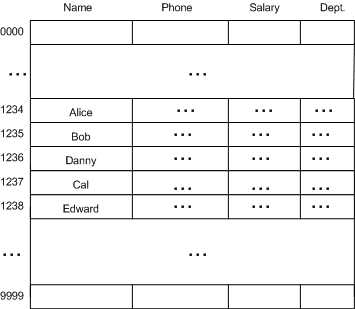
元素的插入过程:
线性探查(Linear Probing)方式虽然简单,但并不是解决冲突的最好的策略,因为它会导致同类哈希的聚集(Primary Clustering)。这导致搜索哈希表时,冲突依然存在。例如上面例子中的哈希表,如果我们要访问 Edward 的信息,因为 Edward 的社保号 111-00-1235 哈希为 1235,然而我们在 1235 位置找到的是 Bob,所以再搜索 1236,找到的却是 Danny,以此类推直到找到 Edward。
一种改进的方式为二次探查(Quadratic Probing),即每次检查位置空间的步长为平方倍数。也就是说,如果位置 s 被占用,则首先检查 s + 12 处,然后检查s - 12,s + 22,s - 22,s + 32 依此类推,而不是象线性探查那样以 s + 1,s + 2 ... 方式增长。尽管如此,二次探查同样也会导致同类哈希聚集问题(Secondary Clustering)。
另一种改进的开放寻址法称为二度哈希(Rehashing)(或称为双重哈希(Double Hashing))。
二度哈希的工作原理如下:
有一个包含一组哈希函数 H1...Hn 的集合。当需要从哈希表中添加或获取元素时,首先使用哈希函数 H1。如果导致冲突,则尝试使用 H2,以此类推,直到 Hn。所有的哈希函数都与 H1 十分相似,不同的是它们选用的乘法因子(multiplicative factor)。
在 .NET 中 Hashtable 类的哈希函数 Hk 的定义如下:
Hk(key) = [GetHash(key) + k * (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1)))] % hashsize
当使用二度哈希时,重要的是在执行了 hashsize 次探查后,哈希表中的每一个位置都有且只有一次被访问到。也就是说,对于给定的 key,对哈希表中的同一位置不会同时使用 Hi 和 Hj。在 Hashtable 类中使用二度哈希公式,其始终保持 (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1)) 与 hashsize 互为素数(两数互为素数表示两者没有共同的质因子)。
二度哈希使用了 Θ(m2) 种探查序列,而线性探查(Linear Probing)和二次探查(Quadratic Probing)使用了Θ(m) 种探查序列,故二度哈希提供了更好的避免冲突的策略。
向 Hashtable 中添加新元素时,需要检查以保证元素与空间大小的比例不会超过最大比例。如果超过了,哈希表空间将被扩充。步骤如下:
由此看出,对哈希表的扩充将是以性能损耗为代价。因此,我们应该预先估计哈希表中最有可能容纳的元素数量,在初始化哈希表时给予合适的值进行构造,以避免不必要的扩充。
链接技术(chaining)是一种冲突解决策略(Collision Resolution Strategy)。在链接法中,把哈希到同一个槽中的所有元素都放到一个链表中。
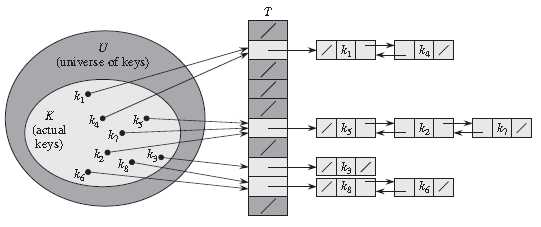
使用探查技术(probing)时,如果发生冲突,则将尝试列表中的下一个位置。如果使用二度哈希(rehashing),则将导致所有的哈希被重新计算。而链接技术(chaining)将采用额外的数据结构来处理冲突,其将哈希表中每个位置(slot)都映射到了一个链表。当冲突发生时,冲突的元素将被添加到桶(bucket)列表中,而每个桶都包含了一个链表以存储相同哈希的元素。
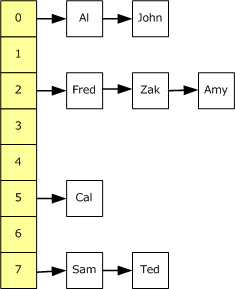
上图中的哈希表包含了 8 个桶(bucket),也就是自顶向下的黄色背景的位置。如果一个新的元素要被添加至哈希表中,将会被添加至其 Key 的哈希所对应的桶中。如果在相同位置已经有一个元素存在了,则将会将新元素添加到列表的前面。
使用链接技术添加元素的操作涉及到哈希计算和链表操作,但其仍为常量,渐进时间为 O(1)。而进行查询和删除操作时,其平均时间取决于元素的数量和桶(bucket)的数量。具体的说就是运行时间为 O(n/m),这里 n 为元素的总数量,m 是桶的数量。但通常对哈希表的实现几乎总是使 n = O(m),也就是说,元素的总数绝不会超过桶的总数,所以 O(n/m) 也变成了常量 O(1)。
一个好的哈希函数应满足假设:每个关键字都等可能地被哈希到 m 个槽位的任何一个之中,并且与其他的关键字已被哈希到哪一个槽位中无关。不幸的是,通常情况下不太可能检查这一条件是否成立,因为人们很少能知道关键字所符合的概率分布,而各关键字可能并不是完全互相独立的。在实践中,常常运用启发式技术来构造好的哈希函数。比如在设计中,可以利用有关关键字分布的限制性信息等。
除法哈希法和乘法哈希法属于启发式的方法,而全域哈希法则采用了随机化技术来获取良好的性能。
一种好的哈希做法是以独立于数据中可能存在的任何模式的方式导出哈希值。例如,除法哈希法用一个特定的质数来除所给的关键字,所得的余数即为该关键字的哈希值。
除法哈希函数可表示为:
hash(key) = key mod m
其中 key 表示被哈希的关键字,m 表示哈希表的大小,mod 为取余操作。假定所选择的质数与关键字分布中的任何模式都是无关的,这种方法常常可以给出很好的结果。
乘法哈希法(The Multiplication Method)
乘法哈希函数可表示为:
hash(key) = floor( m * ( A * key mod 1) )
其中 floor 表示对表达式进行下取整,常数 A 取值范围为(0<A<1),m 表示哈希表的大小,mod 为取余操作。[A * key mod 1] 表示将 key 乘上某个在 0~1 之间的数并取乘积的小数部分,该表达式等价于 [A*key - floor(A * key)]。
乘法哈希法的一个优点是对 m 的选择没有什么特别的要求,一般选择它为 2 的某个幂次,这是因为我们可以在大多数计算机上更方便的实现该哈希函数。
虽然这个方法对任何的 A 值都适用,但对某些值效果更好,最佳的选择与待哈希的数据的特征有关。Don Knuth 认为 A ≈ (√5-1)/2 = 0.618 033 988... 比较好,可称为黄金分割点。
在向哈希表中插入元素时,如果所有的元素全部被哈希到同一个桶中,此时数据的存储实际上就是一个链表,那么平均的查找时间为 Θ(n) 。而实际上,任何一个特定的哈希函数都有可能出现这种最坏情况,唯一有效的改进方法就是随机地选择哈希函数,使之独立于要存储的元素。这种方法称作全域哈希(Universal Hashing)。
全域哈希的基本思想是在执行开始时,从一组哈希函数中,随机地抽取一个作为要使用的哈希函数。就像在快速排序中一样,随机化保证了没有哪一种输入会始终导致最坏情况的发生。同时,随机化也使得即使是对同一个输入,算法在每一次执行时的情况也都不一样。这样就确保了对于任何输入,算法都具有较好的平均运行情况。
hasha,b(key) = ((a*key + b) mod p) mod m
其中,p 为一个足够大的质数,使得每一个可能的关键字 key 都落在 0 到 p - 1 的范围内。m 为哈希表中槽位数。任意 a∈{1,2,3,…,p-1},b∈{0,1,2,…,p-1}。
当关键字的集合是一个不变的静态集合(Static)时,哈希技术还可以用来获取出色的最坏情况性能。如果某一种哈希技术在进行查找时,其最坏情况的内存访问次数为 O(1) 时,则称其为完美哈希(Perfect Hashing)。
设计完美哈希的基本思想是利用两级的哈希策略,而每一级上都使用全域哈希(Univeral Hashing)。
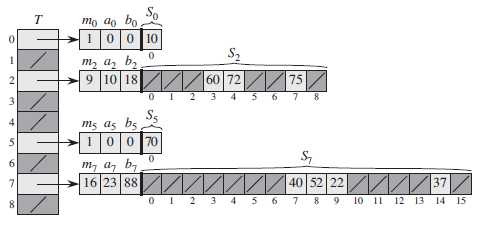
第一级与使用链接技术(chaining)的哈希表基本上是一样的,利用从某一全域哈希函数族中随机选择的一个函数 h ,将 n 个关键字哈希到 m 个槽中。
而此时,不像链接技术中对槽使用链表结构,而是采用一个较小的二次哈希表 Sj ,与其相关的哈希函数为 hj 。通过随机的选取哈希函数 hj ,可以确保在第二级上不出现哈希冲突。
如果利用从一个全域哈希函数族中随机选择的哈希函数 h,将 n 个关键字存储在一个大小为 m = n2 的哈希表中,那么出现碰撞的概率小于 1/2 。
为了确保第二级上不出现哈希冲突,需要让哈希表 Sj 的大小 mj 为哈希到槽 j 中的关键字数 nj 的平方。mj 对 nj 的这种二次依赖关系看上去可能使得总体存储需求很大,但通过适当地选择第一次哈希函数,预期使用的的总存储空间仍为 O(n)。
如果关键字的数量 n 等于槽的数量 m ,则该哈希函数称为最小完美哈希函数(Minimal Perfect Hash Function)。
参考资料
本文《哈希表和完美哈希》由 Dennis Gao 发表自博客园博客,任何未经作者本人允许的人为或爬虫转载均为耍流氓。
原文:http://www.cnblogs.com/gaochundong/p/hashtable_and_perfect_hashing.html