题目连接:Sherlock and MiniMax
Watson gives Sherlock an array A1,A2...AN.
He asks him to find an integer M between P and Q(both inclusive), such that, min {|Ai-M|, 1 ≤ i ≤ N} is maximised. If there are multiple solutions, print the smallest one.
Input Format
The first line contains N. The next line contains space separated N integers, and denote the array A. The third line contains two space separated integers denoting P and Q.
Output Format
In one line, print the required answer.
Constraints
1 ≤ N ≤ 102
1 ≤ Ai ≤ 109
1 ≤ P ≤ Q ≤ 109
Sample Input
3
5 8 14
4 9
Sample Output
4题解:难度为Diffcult的一道题,真的好难=。=
首先题目理解:给定一个数组a和两个整数P和Q,在区间[P,Q]中找到一个数M,使得min{a[i] - M}最大,即对于每一个[P,Q]之间的数m,将数组中的每个数和m求差的绝对值,那么这些绝对值里面就有一个最小值(比如题目中的例子,选择m=4,那么对应的3个差的绝对值是1,4,10,最小值就是1)。现在要做的就是选出这个m,使得这个最小值最大(比如如果选定m=5,那么对应的3个差的绝对值是0,3,9,最小值是0,就比刚才选4的时候得到的最小值小,所以m选4不选5)。
首先对原数组排序,那么对于[P,Q]之间的任意一个m,对应的差的绝对值如下图两种情况所示:

图一
在第一种情况中,最小值在端点处达到;在第二种情况中,最小值在转折点处达到,这都是由a数组有序以后得到的性质。那么我们想想在哪些地方可以达到最大的最小值。如小图所示,对于任意两个数,当且仅当取m为它们的中点(a[i]+a[i+1])/2的时候,得到的最小绝对值最大。所以就可以遍历所有的(a[i],a[i+1]),然后找出使得最小值最大的m作为M。
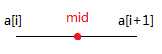
图二
在这个过程中,有一种情况就是(a[i],a[i+1])的中点不在[P,Q]内,那么最小值或者在[P,Q]中最靠近中点处取得(区间[P,Q]和区间[a[i],a[i+1]]有交集时候,在P或者Q取到最小值);或者[P,Q]和[a[i],a[i+1]]没有交集,即图一中第一种情况,最小值也在P或者Q处达到。那么我们为单独用O(n)的时间考察P和Q,遍历数组,找到最小值,然后查看是否可能成为最大的最小值。
总结一下算法:
代码如下:
1 import java.io.*; 2 import java.util.*; 3 import java.math.*; 4 5 6 public class Solution { 7 static int miniMax = 0; 8 static int miniMax_index = 0; 9 private static int mini_first_last(int[] a,int first_last){ 10 //check for p 11 int mini = Integer.MAX_VALUE; 12 13 for(int i = 0;i < a.length;i++){ 14 mini = Math.min(mini,Math.abs(a[i]-first_last)); 15 } 16 17 return mini; 18 } 19 private static void middle(int index,int[] a,int p,int q){ 20 int mini = Integer.MAX_VALUE; 21 int mini_index = 0; 22 int mid = (a[index]+a[index+1])/2; 23 if(mid >= p && mid <= q){ 24 int m = Math.abs(a[index]-mid); 25 int n = Math.abs(a[index+1]-mid); 26 if(mini > Math.min(m, n)){ 27 mini = Math.min(m, n); 28 mini_index = mid; 29 } 30 if(mid+1<=q && mid*2 != a[index] + a[index+1]){ 31 m = Math.abs(a[index]-mid-1); 32 n = Math.abs(a[index+1]-mid-1); 33 if(mini > Math.min(m, n)){ 34 mini = Math.min(m, n); 35 mini_index = mid+1; 36 } 37 } 38 if(mini != Integer.MAX_VALUE && miniMax < mini){ 39 miniMax = mini; 40 miniMax_index = mini_index; 41 } 42 } 43 44 } 45 public static void main(String[] args) { 46 Scanner in = new Scanner(System.in); 47 int n = in.nextInt(); 48 int[] a = new int[n]; 49 for(int i = 0;i < n;i++) 50 a[i] = in.nextInt(); 51 int p = in.nextInt(); 52 int q = in.nextInt(); 53 Arrays.sort(a); 54 55 miniMax = mini_first_last(a, p); 56 miniMax_index = p; 57 58 int temp = mini_first_last(a, q); 59 if(miniMax < temp){ 60 miniMax = temp; 61 miniMax_index = q; 62 } 63 64 for(int i = 0;i < n-1;i++){ 65 middle(i, a, p, q); 66 } 67 System.out.println(miniMax_index); 68 } 69 }
【HackerRank】Sherlock and MiniMax,布布扣,bubuko.com
【HackerRank】Sherlock and MiniMax
原文:http://www.cnblogs.com/sunshineatnoon/p/3888891.html