主成分分析（PCA）学习笔记

一、PCA基本思路

　　将数据从原来的坐标系转换到新的坐标系，新坐标系的选择由数据本身决定。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选择的是和第一个坐标轴正交且具有最大方差的方向，依次类推，直到找出\(k\)个新坐标轴。也就是将原始数据投影到一个低维的坐标系中。

二、PCA目标函数

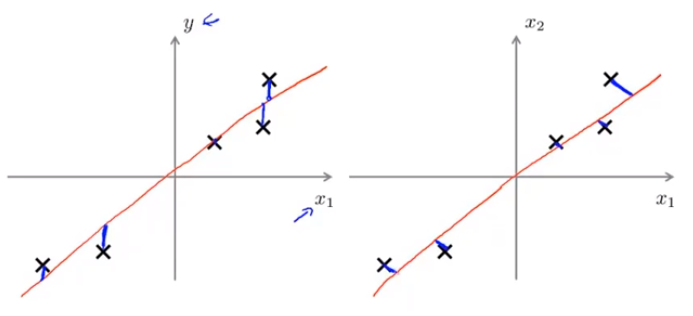
　　以最小化投影误差为目标函数，这里注意与线性回归的区别，线性回归是最小化垂直距离。下图左边图中蓝线是线性回归的目标，右图中蓝线是PCA的目标。

三、PCA算法步骤

1、数据预处理，数据维度为 $ m*n $ 。

　　对 $ X= x^{(1)}, x^{(2)}, ... , x^{(m)} $ 去平均值，\[ u_j = \frac{1}{m}\sum_{i=1}^{m}x_j^{(i)} \] \[ s_j = \frac{1}{m}\sum_{i=1}^{m}(x_j^{(i)}-u_j)^2 \]
对原始数据进行归一化处理得到 \[ x_j = \frac{x_j-u_j}{s_j} \]
其中 $ u_j $ 表示均值， $ s_j $ 表示方差。

2、计算协方差矩阵 $ \Sigma $ 。

\[ \Sigma = \frac{1}{m} \sum_{i=1}^{m}(x^{(i)}.(x^{(i)})^T) \]
　　其中 $ x^{(i)} $ 是 $ n \times 1 $ 维的，则其转秩是$ 1 \times n $ 维的，所以 $ \Sigma $ 是 $ n \times n $ 维的。

3、对 $ \Sigma $ 进行奇异值分解。

\[ U,S,V = svd(\Sigma) \]
奇异值分解可以参考博客，博主讲的比较清楚。上式中
\[ U = [u^{(1)}, u^{(2)},...,u^{(n)}]\in R^{n*n} \]
从中选取 $ k $ 个主要成分
\[ U_k = [u^{(1)}, u^{(2)},...,u^{(k)}] \]
则 $ x^{(i)} $ 在新坐标上的投影可以表示为
\[ z^{(i)} = [u^{(1)}, u^{(2)},...,u^{(k)}]^T\cdot x^{(i)}= \begin{bmatrix} u^{(1)}\\ u^{(2)}\\ \vdots \\ u^{(k)}\\end{bmatrix}\cdot x^{(i)} \]
其中 $ U_k $ 是 $ k \times n $ 维的，其转秩为 $ n \times k $ 维的，$ x^{(i)} $ 是 $ n \times 1 $ 维，所以 $ z^{(i)} $ 是 $ k \times 1 $ 维的。投影 $ Z $ 可以表示为
\[ Z = U_k^T \cdot X \]

4、计算重构后特征 $ x_{approx}^{(i)} $ 。

\[ x^{(i)}_{approx} = U_k \cdot z^{(i)} \]
其中 $ U_k $ 是 $ n \times k $ 维，$ z^{(i)} $ 是 $ k \times 1 $ 维，则 $ x_{approx}^{(i)} $ 是 $ n \times 1 $ 维。

5、根据投影误差检验选择的 $ k $ 个主要成分是否满足要求。

\[ \frac{\frac{1}{m}\sum_{i=1}^{m}||x^{(i)}-x^{(i)}_{approx}||^2}{\frac{1}{m}\sum_{i=1}^{m}||x^{(i)}||^2} \leq 0.01 \]
如果不满足上式，则从步骤3中重新选择 $ k $ 个主成分，继续第4和第5步，知道满足要求。小于等于0.01表明保留了原始数据99%信息，这里可以根据需求进行更改。
这里如果不用奇异值分解后的 $ U $ 矩阵，也可以根据奇异值矩阵 $ S $ 计算 ，$ S $ 是主对角线上为从大到小排列的奇异值，其他元素全为0的对角矩阵。
\[ 1-\frac{\sum_{i=1}^{k}S_{ii}}{\sum_{i=1}^{n}S_{ii}}\leq 0.01 \]

PCA应用实例

1、二维数据投影到一维，熟悉PCA流程

第一步 引入相关库并导入数据

from scipy.io import loadmat
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data1 = loadmat(‘./ex7/ex7data1.mat‘)
data1

X = data1[‘X‘]
X.shape

原始数据展示

plt.scatter(X[:,0], X[:,1])
plt.show()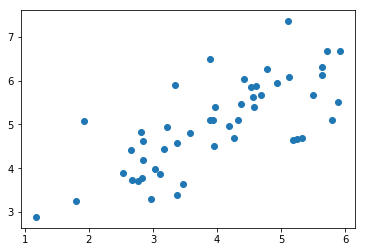

第二步 数据预处理

# 定义归一化函数featureNormalize
def featureNormalizse(x):
    mean = x.mean(axis=0)
    std = x.std(axis=0)
    return (x-mean)/std, mean, std

# test
x_norm, means, stds = featureNormalizse(X)
x_norm[:5]

第三步 计算协方差矩阵

print(x_norm.shape)
sigma = (x_norm.T.dot(x_norm))/x_norm.shape[0]
sigma

第四步 奇异值分解

U,S,V = np.linalg.svd(sigma)
U,S,V

# 整合sigma和svd
def pca(x):
    sigma = (x.T.dot(x))/x.shape[0]
    U,S,V = np.linalg.svd(sigma)
    return U,S,V

可视化主成分

x_norm, means, stds = featureNormalizse(X)
U, S, V = pca(x_norm)

plt.figure(figsize=(8, 6))
plt.scatter(X[:,0], X[:,1], label=‘sample data‘)  # 样本数据点

plt.plot([means[0], means[0] + 1.5*S[0]*U[0,0]], 
         [means[1], means[1] + 1.5*S[0]*U[0,1]],
        c=‘r‘, linewidth=3, label=‘First Principal Component‘)  # 第一个成分
plt.plot([means[0], means[0] + 1.5*S[1]*U[1,0]], 
         [means[1], means[1] + 1.5*S[1]*U[1,1]],
        c=‘g‘, linewidth=3, label=‘Second Principal Component‘)  # 第二个成分

plt.grid()
plt.axis("equal")  
plt.legend()
plt.show()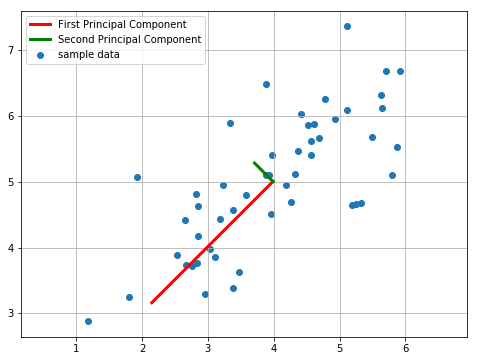

第五步 计算 $ x_{approx} $

# 根据U_reduce计算x_norm的投影Z
def compute_z(X, U, k):
    Z = X.dot(U[:,:k])
    return Z

# test
Z = compute_z(x_norm, U, 1)
Z[:5]

# 计算x_approx
def compute_x_approx(U, k, Z):
    x_approx = Z.dot(U[:,:k].T)  # 50*1 * 1*2
    return x_approx

# test
x_approx = compute_x_approx(U, 1, Z)
x_approx[:5]

第六步 可视化投影效果

plt.figure(figsize=(8,6))
plt.axis("equal") 
plot = plt.scatter(x_norm[:,0], x_norm[:,1], s=30, facecolors=‘none‘, 
                   edgecolors=‘b‘,label=‘Original Data Points‘)  # 画出归一化后原始样本点
plot = plt.scatter(x_approx[:,0], x_approx[:,1], s=30, facecolors=‘none‘, 
                   edgecolors=‘r‘,label=‘PCA Reduced Data Points‘)  # 画出经过PCA后构造的估计值

plt.title("Example Dataset: Reduced Dimension Points Shown",fontsize=14)
plt.xlabel(‘x1 [Feature Normalized]‘,fontsize=14)
plt.ylabel(‘x2 [Feature Normalized]‘,fontsize=14)
plt.grid(True)

for x in range(x_norm.shape[0]):  # 画出变换前后的连线
    plt.plot([x_norm[x,0],x_approx[x,0]],[x_norm[x,1],x_approx[x,1]],‘k--‘)
    # 输入第一项全是X坐标，第二项都是Y坐标
plt.legend()
plt.show()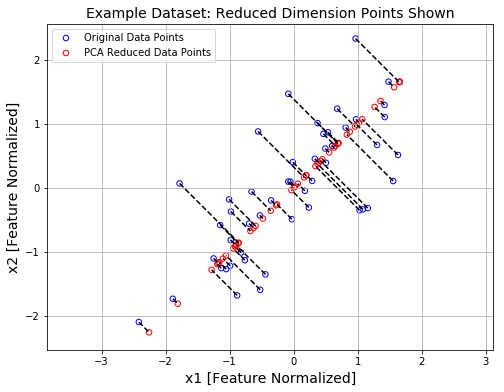

2、利用PCA减少图片维度

第一步 导入数据

# 导入数据
face_data = loadmat(‘./ex7/ex7faces.mat‘)
face = face_data[‘X‘]
face.shape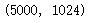

第二步 展示数据

def showFace(X, row, col):
    fig, axs = plt.subplots(row, col, figsize=(8,8))
    for r in range(row):
        for c in range(col):
            axs[r][c].imshow(X[r*col + c].reshape(32,32).T, cmap = ‘Greys_r‘)
            axs[r][c].set_xticks([])
            axs[r][c].set_yticks([])
            
showFace(face, 10, 10)
plt.show()

第三步 降维并重构

face_norm, means, stds = featureNormalizse(face) # 归一化
U, S, V = pca(face_norm)  # 奇异值分解
Z = compute_z(face_norm, U, 16)  # 计算Z
face_approx = compute_x_approx(U, 16, Z) # 计算降维重构后的数据
face_approx.shape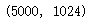

第四步 前后对比图

showFace(face, 10, 10)
showFace(face_approx, 10, 10)
plt.show()