线段树原理
线段树是一颗二叉树,他的每个节点对应的都是一个区间,主要是通过对区间的分割和合并来修改节点的值, 然后再得到答案。
现在给你一个 目的为求区间和 所造出来的线段树 线段树。如下图所示。
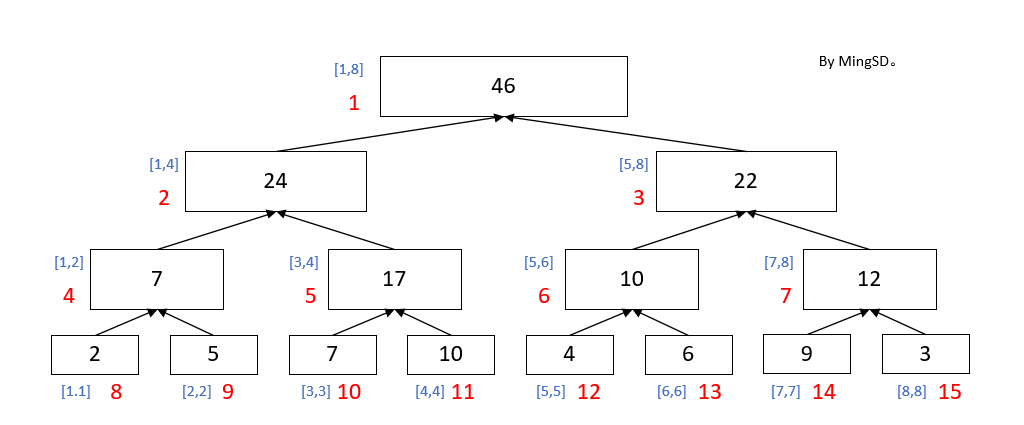
仔细观察,第一二三行方框内的值是他的下面2个子区间的和, 第四行的方框内的数字代表的是自身的值, 蓝色代表的是这个方框他包含的区间, 红色代表的是这个元素在数组中所储存的位置。(在绝大多数博客中,我们默认区间的左儿子他的下标是当前区间下标的2倍,右儿子的下标是当前区间的2倍再加上1,这个下标是认为定义的,你也可以将对应关系修改)。
为什么说用线段树可以节省求和时间呢, 假设我们需要查找区间 [1,8] 的和, 对于这个不用多说, 我们可以直接将最上面的那个46输出,因为最上面的那个矩形代表的就是区间 [1,8] 的和。
然后假设我们要查找区间 [3,7] 的和, 刚开始我们出现在区间 [1,8]的位置, 但是对于目标区间来说 [1,8] 太大了, 所以我们要继续往下走, 走到 [1,4] 和 [5,8] 的区间, 但是对于这2个区间来说, 还有一部分区域是落在查询区间之外的, 所以我们需要继续往下走,我们先分析区间 [1,4] , 对于他左儿子的区间[1,2]来说,没有任意一个点是落在查询区间内的, 所以我们不需要走到他的左儿子处, 然后走到右儿子[3,4],可以发现 [3,4] 倍查询区间覆盖了, 所以我们就不需要往下走了, 因为整个区间都倍覆盖了, 直接将这个点的值返回就好了, 因为这个点就是他下面节点的和。 然后我们再看区间[5,8], 先往左走, 走到左儿子区间 [5,6] ,也可以发现该区间倍查询区间覆盖了,就不需要往下走了, 返回该节点的值,对于右儿子节点 [7,8] 来说,只有一部分区域倍查询区间覆盖, 所以我们还需要往下走,继续往左边走, 发现 [7,7] 是合法区域, 返回该值, {8,8]不是合法区域,所以不对这快里的数据进行处理。 所以最后的结果就是 [3,4] + [5,6] + [7,7] 这3个区间的和。 可能你会说就5个点而已, 我直接加过去时间也就这样, 的确, 当点数小的时候线段树的优势并不会很明显,但是如果查询的区间长度会到达 1e5的话, 那么线段树就可以省下很多时间了。
线段树的某段区间内的值是可以修改的。
假设我们修改了区间[2,2]的值
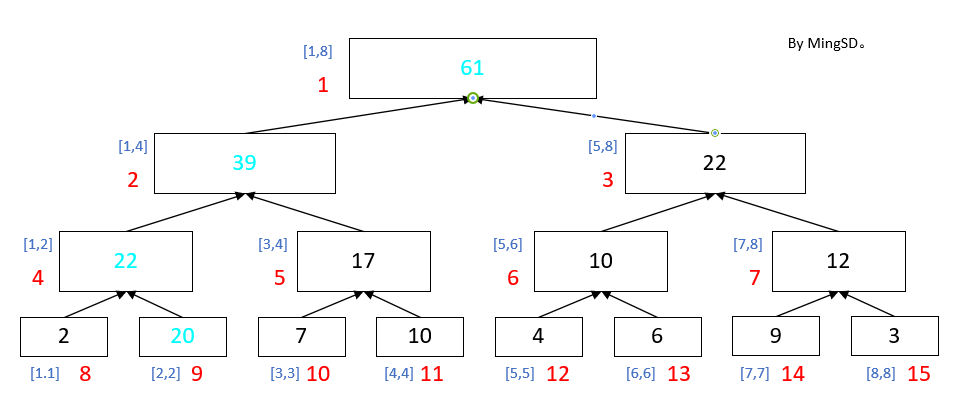
我们就需要更新一下所有区间内含2的区间, 也就是顺着[2,2]一直往上走 按次序更新 [2,2] -> [1,2] -> [1,4] -> [1,8] 这四个区间的值, 更新完了之后就可以继续愉快的去查询区间和了。
可以发现, 每一次对于一个点更新之后, 她执行的点的数目就是logn个, 如果你使用的是前缀和去写的话, 就需要约更新n 个节点。
代码实现
1,建树,对于一颗树需要先建树。这里用到的是递归建树。
 建树(有注释)
建树(有注释) 建树(无注释)
建树(无注释)
2,通过子节点来更新目前节点。
 PushUp(有注释)
PushUp(有注释) PushUp(无注释)
PushUp(无注释)
3,更新某个节点。
 单点更新(有注释)
单点更新(有注释) 单点更新(无注释)
单点更新(无注释)
4, 查询区间和
查询的规则前面已经解释过一次了。
 区间查询(有注释)
区间查询(有注释) 区间查询(无注释)
区间查询(无注释)
总结
1。首先对于大多数线段树题目来说, 第一步就是建树。 建树用法 Build(1,n,1), [1,n]就是第一个节点所代表的区间长度。
2。在每次更新了点之后,为了保证线段树性质, 一定要去执行PushUP操作,保证线段树的性质不丢失。
3。线段树的精华就是,每一个节点代表着一段区间,这个节点的值,就是他所代表的区间内的值。
4。当底层节点只有5个点的时候, 我们处理线段树时, 需要将他变成8个节点, 如果给9个节点, 那么底层节点必须要有16个节点, 所以为了保证空间足够用,所以需要将空间开大2倍,然后由于每一层的上方都还有 m/2个点(m为该层节点的数目)。
所以空间需要再大两倍, 最终合起来就是4倍。 所以我们需要开 4n 的空间。
HDU-1166 线段树求区间和
 View Code
View CodeHDU-1754 线段树求区间最大值
 View Code
View Code
区间更新 lazy标记
现在我们突然遇到这样一个题目
这个题目和上面题目不同的地方是更新, 在这个题目中, 他更新数据是成段更新, 上面的题目都是一个点一个点更新, 并且更新的次数不是很少, 我们不可能去像点更新一样, 将这些区域内的点都一个个更新过去。
前面提到过,线段树的每一个节点都代表着一段区间的性质, 所以假如我们需要对于区间 [5,8] 里面的数都加上 10。(基于更新[2,2]后的那个线段树)。
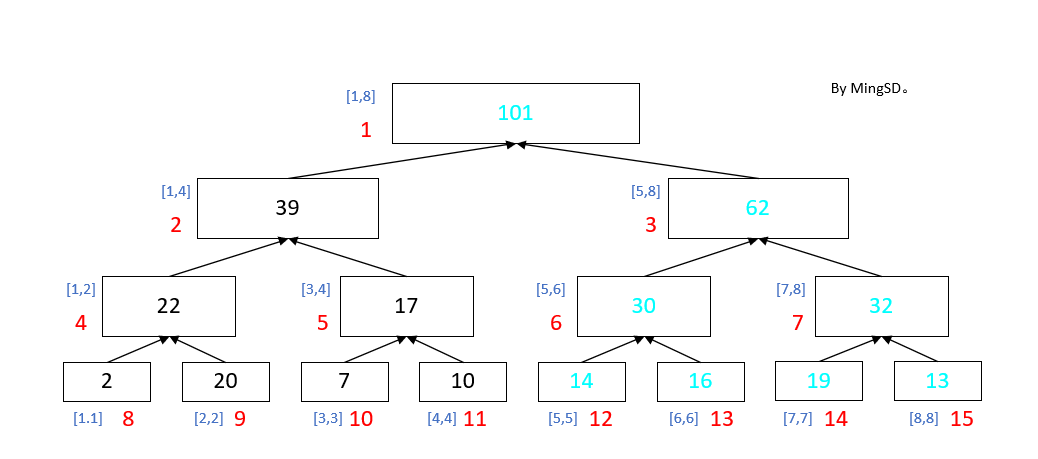
如果我们将一个个点覆盖过去之后, 现在的这课树是这样的。
我们可以发现对节点3来说, 他所管辖的区间[5,8]都是要被更新的区间,并且他增加的指为40,即 区间长度(4) * 修改的值(10)。 我们可以发现,在区域更新的时候, 对于一个节点来说, 如果他所管理的区间 被 要更新的区间 覆盖了, 那我们就提早了知道这一个节点的值。
然后我们引入一个概念, lazy标记, 还是对于开头的情况来说, 如果我们使用了lazy标记之后, 这一课线段树是这样的
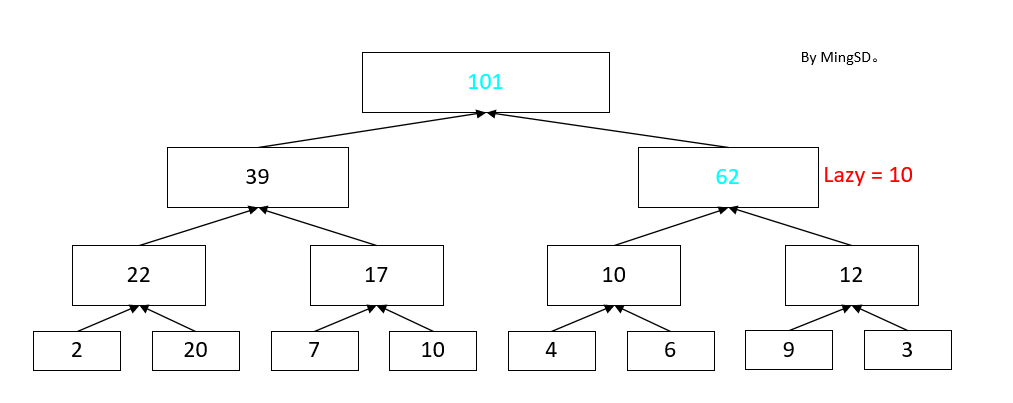
在这一颗树上, 我们只修改了2个节点, 同时在节点3处增加了一个 lazy标记, 在这个标记中 lazy = 10。(即整段区间内每一个点都要加上的值)。接下来, 我们如果询问区间[1,8]的和, 我们直接返回节点1就好了。 如果我们询问区间 [3,8] 的和 那么只需要返回 [3,4] + [5,8] 的值。 我们可以看见如果不访问[5,8]的子区间的时候, 我并不会用到里面的值。 在这些时候, 我们并不需要更新里面的值, 更不更新都一样, 不会被访问到。
如果我们现在需要查询 [1,5]的和, 我们只需要将 lazy 标记下推,然后再更新对应的区间就好了。
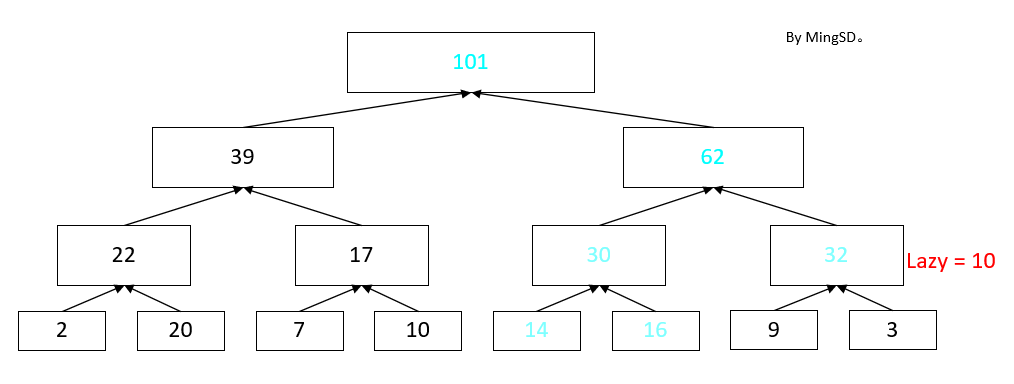
然后我们返回 [1,4] + [5,5] 的值就好了。
总结就是:
lazy标记的含义就是延迟更新,在我们不需要访问区间内部时就保留lazy标记的值,如果需要访问内部的时候,我们要先将lazy标记下推, 因为可能lazy标记还需要继续往下走。
在区域更新的时候,如果 当前区间 被 更新的区间完全覆盖了, 就直接在这个节点加上 区间长度*修改的值, 并且更新这个点的lazy标记。
操作代码:
PushDown --- 将lazy标记下推
 PushDown
PushDown 区域更新
区域更新 查询
查询注意的就是每次对子区间进行修改的时候,我们都需要提前先把lazy标记下推。
所以一开始的那个题目我们就可以做了。
 POJ-3468
POJ-3468再来一道
 HDU-1698
HDU-1698
到此关于线段树的查询 单点更新 区域更新都介绍完了。
还有一种特殊的思想是: 线段树求逆序对。
