杨辉三角,也算是一个经典的题目了。就简单的说说。
写代码之前,先分析要做的东西的特点,找到规律,再把这个规律描述一下。
然后把这个描述翻译成编程语言,就可以说是编程了。
那么杨辉三角有什么特点?
首先是个三角(感觉这是屁话,但也得说),在数学里边,我们手写画出来,就像一个等腰三角形。
而在计算里边,打印个等腰三角形,还真不不太容易,好在三角的形状不是我们关注的重点,所以,我们这个三角形,是直角三角形,腰没了。
这个三角形有还有什么特点呢?
先是元素个数,这个有个特点,就是当前是第几行,那么这行就会有几列,比如,第一行,那么只有一列,第二行,就有两列,第三行有三列……
还有顶点(前两行)和两边,都是1,并且所有对称,每一行如果是一个字符串的话, 这就属于一个回文串。
那什么是回文串?可不是回族文字的字符串啊,是正读反读都是一样的字符串。比如:123454321,abcdedcba等等
那么再看看,还有其他特点么?
答案是肯定的,还有一个特点就是,从第三行开始,每行(除了第一个和最后一个)数字,都是上一行,同列的值加上上一行前一列的值的和。
到这里,基本上就算是分析完了。理论上,我们把这些翻译成代码,这也就算写完了。
但是任何语言的翻译,都是要再修饰,太直白的翻译,硬!所以,后续根据情况,还要做些优化。
尝试写代码:
1、三角形(直角),其实就是一个长方形对角线的一半。可以理解成一个二维数组,一半有值,一半空。
const LINES int = 10; var yh [LINES][LINES]int;
这样就定义了一个10行,10列的数组
矩阵有了,还要有坐标。因为要用循环来操作嘛,循环的时候,二维数组我们习惯用“i”和“j”来做下标,我们也顺便把两个变量看成坐标。i就是行,j就是列。
2、顶点(前两行)和两边都是1,从第三行开始,每行(除了第一个和最后一个)数字,都是上一行,同列的值加上上一行前一列的值的和
if i < 2 {//两行以内三角中的数字都是1
yh[i][j] = 1;
}else{//第三行开始,正式计算数值写入数组
if j == 0 || j == i {
yh[i][j] = 1;//所有行的第一列和最后一列都是1
}else{
yh[i][j] = yh[i-1][j-1] + yh[i-1][j];//当前数组元素是上一行的前一个元素加上上一行的当前列元素
}
}
上边,这段代码,同样是翻译了之前的一段描述,也就是杨辉三角的特点。到此为止,我们的代码关键部分基本完成了,还有哪里呢?
想想,哦~~还有个第几行,就是第几列。二维数组嘛,半个三角。那么如何写呢?
for i := 0; i < LINES; i++ {//LINE行
for j := 0; j < i + 1; j++ {//有几行,就有几列
//代码片段
}
}
以上代码,就是用到的循环。那么到这里,所有的代码翻译完成。这样就把这个杨辉三角完成了。
在循环过程中,可以输出数据,配合格式符,就是一个三角。
循环结束,数组的下标,就是杨辉三角的坐标,可以根据坐标,返回对应坐标的数字。
下边是完整代码:
package main;
import (
"fmt"
);
const LINES int = 10;//设定杨辉三角10行,同时也相当于10列
func ShowYanghui(){
var yh [LINES][LINES]int;
for i := 0; i < LINES; i++ {
for j := 0; j < i + 1; j++ {
if i < 2 {//两行以内三角中的数字都是1
yh[i][j] = 1;
}else{//第三行开始,正式计算数值写入数组
if j == 0 || j == i {
yh[i][j] = 1;//所有行的第一列和最后一列都是1
}else{
yh[i][j] = yh[i-1][j-1] + yh[i-1][j];//当前数组元素是上一行的前一个元素加上上一行的当前列元素
}
}
fmt.Printf("%d\t", yh[i][j] );//格式化输出一行
}
fmt.Print("\n");//换行
}
}
func main(){
ShowYanghui();
};
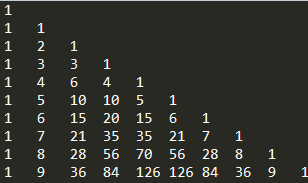
输出效果:
原文:https://www.cnblogs.com/leafinwind/p/10290125.html