霍夫曼树是二叉树的一种特殊形式,又称为最优二叉树,其主要作用在于数据压缩和编码长度的优化。
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
从树根到每一个结点的路径长度之和。
从该节点到树根之间的路程长度与节点权重的乘积
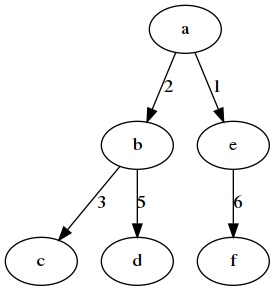
树中所有节点的带权路径长度之和,称为WPL
带权路径长度WPL最小的二叉树称为哈夫曼树
假设有abcde 5个节点,它们的权重分别是5,15,40,30,10.
1. 我们先把有权重的叶子节点按照从小到大的顺序排列成一个有序数列,即:a5,e10,b15,d30,c40
2. 取前两个最小权重的节点作为一个新的节点N1的两个子节点,相对较小的是左孩子,这里就是a为N1的左孩子,e为N1的右孩子,新的权值为两个叶子权值的和5+10=15
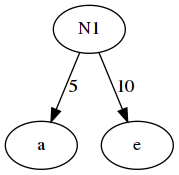
3. 将N1替换a和e,插入有序序列中,保持从小到大的排列。即:N1-15,b15,d30,c40
4. 重复步骤2,将N1与b作为一个新的节点N2的两个子节点。N2的权值为15+15=30
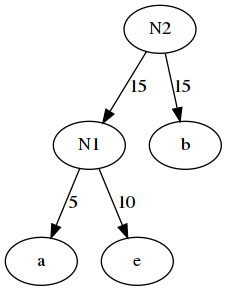
5. 将N2替换N1与b,插入有序序列中,保持从小到大的排列,即:N2-30,d30,c40
6. 重复步骤2。将N2与d作为一个新的节点N3的两个子节点。N3的权值为30+30=60
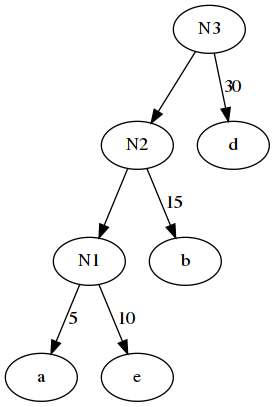
7. 最终效果如图
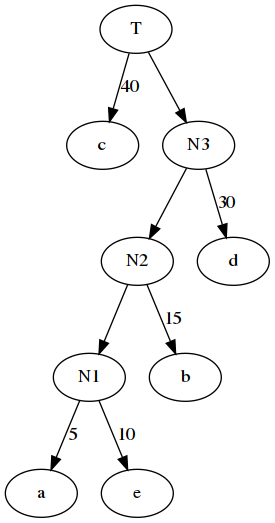
这棵树的带权路径长度为 40x1+30x2+15x3+10x4+5x4=205
通过上面的构造过程,我们可以得出构造哈夫曼树的哈夫曼算法描述
1. 根据给定的n个权值{w1,w2,...,wn}构成n棵二叉树的集合F={T1,T2,...,Tn},其中每棵二叉树Ti中只有一个带权为wi根节点,其左右子树均为空
2. 在F中选取两个根节点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和
3. 在F中删除这两棵树,同时将新得到的二叉树加入F
4. 重复步骤2和3,直到F只含一棵树为止。这棵树就是哈夫曼树
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
struct haffman_node_s
{
char label;
int value;
haffman_node_s *left;
haffman_node_s *right;
haffman_node_s(char lbl, int data):label(lbl),value(data),left(nullptr),right(nullptr) {}
};
haffman_node_s *create_haffman_tree(std::vector<char> & label, std::vector<int> & v)
{
int len = v.size();
std::vector<haffman_node_s*> pnodes(len);
for (int i = 0; i < len; i++)
{
pnodes[i] = new haffman_node_s(label[i], v[i]);
}
int idx = 1;
while (pnodes.size() > 1)
{
std::sort(pnodes.begin(), pnodes.end(), [](haffman_node_s* a, haffman_node_s* b){
return a->value < b->value;
});
haffman_node_s* N = new haffman_node_s(idx+‘0‘, pnodes[0]->value + pnodes[1]->value);
N->left = pnodes[0];
N->right = pnodes[1];
pnodes.emplace_back(N);
pnodes.erase(pnodes.begin());
pnodes.erase(pnodes.begin());
idx++;
}
return pnodes[0];
}
void travel(haffman_node_s *root)
{
std::queue<haffman_node_s *> Q;
if (root)
{
Q.push(root);
}
FILE *pf = fopen("hfm.dot", "w");
fprintf(pf, "graph hfm {\n");
fprintf(pf, "\tgraph [ordering=\"out\"];\n");
while (!Q.empty())
{
haffman_node_s *node = Q.front();
Q.pop();
if (node->left)
{
fprintf(pf, "\t%c -- %c[color=\"red\", label=\"%d\"];\n", node->label, node->left->label, node->left->value);
Q.push(node->left);
}
if (node->right)
{
fprintf(pf, "\t%c -- %c[color=\"blue\", label=\"%d\"];\n", node->label, node->right->label, node->right->value);
Q.push(node->right);
}
}
fprintf(pf, "}\n");
fclose(pf);
system("dot hfm.dot -Tpng -o hfm.png");
}
int main()
{
std::vector<char> label {‘a‘, ‘b‘, ‘c‘, ‘d‘, ‘e‘};
std::vector<int> v {5, 20, 40, 30, 10};
haffman_node_s *root = create_haffman_tree(label, v);
travel(root);
return 0;
}
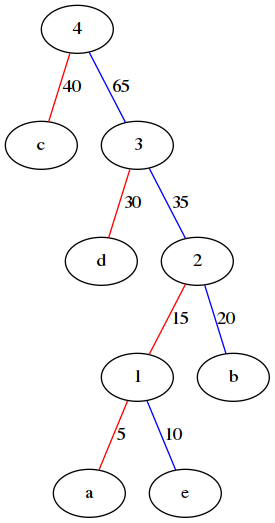
当年哈夫曼研究这个最优树目的是为了解决远距离通信的数据传输最优化问题
比如,我们通过网络传输一段文字"BADCADFEED"给别人。显然使用二进制的数字(0和1)来表示是很自然的想法。因为现在只有6个字母ABCDEF,我们可以用相应的二进制数据表示:
| 字母 | A | B | C | D | E | F |
| 二进制字符 | 000 | 001 | 010 | 011 | 100 | 101 |
这样,真正传输的数据就是编码后的"001000011010000011101100100011",对方接受时按照3位一分来译码。如果一篇文章很长,这样的二进制串也非常大。而事实上,不管是英文、中文还是其他语言,字母或汉字的出现频率是不同的,比如英语中几个元音字母"aeiou",中文的"的了有在"出现的频率都很高
假设以6个字母的频率为 A 27, B 8, C 15, D 15, E 30, F 5,合起来正好是100%。那就意味着,我们完全可以按照哈夫曼树来编码它们。
下图分别是哈夫曼树、权值左分支改为0,右分支改为1后的哈夫曼树:
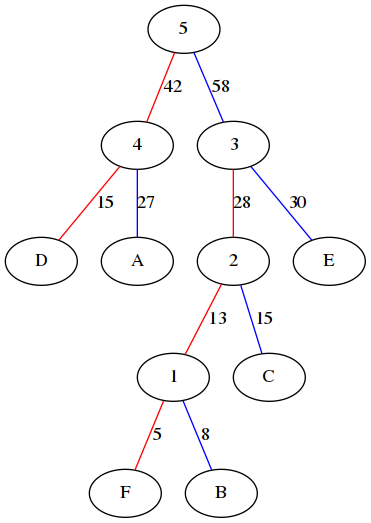
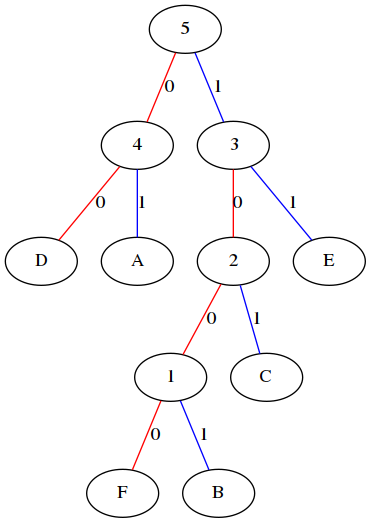
我们将这6个字母用其从树根到叶子节点所经过的路径的01来编码,可以得到如下编码:
| 字母 | A | B | C | D | E | F |
| 二进制字符 | 01 | 1001 | 101 | 00 | 11 | 1000 |
再次将"BADCADFEED"编码,对比如下:
原编码:"001000011010000011101100100011" 30个字符
新编码:“1001010010101001000111100” 25个字符
使用哈夫曼编码,我们的数据被压缩了。
编码和解码代码:
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <unordered_map>
#include <string>
struct haffman_node_s
{
char label;
int value;
haffman_node_s *left;
haffman_node_s *right;
haffman_node_s(char lbl, int data):label(lbl),value(data),left(nullptr),right(nullptr) {}
};
haffman_node_s *create_haffman_tree(std::vector<char> & label, std::vector<int> & v)
{
int len = v.size();
std::vector<haffman_node_s*> pnodes(len);
for (int i = 0; i < len; i++)
{
pnodes[i] = new haffman_node_s(label[i], v[i]);
}
int idx = 1;
while (pnodes.size() > 1)
{
std::sort(pnodes.begin(), pnodes.end(), [](haffman_node_s* a, haffman_node_s* b){
return a->value < b->value;
});
haffman_node_s* N = new haffman_node_s(idx+‘0‘, pnodes[0]->value + pnodes[1]->value);
N->left = pnodes[0];
N->right = pnodes[1];
pnodes.emplace_back(N);
pnodes.erase(pnodes.begin());
pnodes.erase(pnodes.begin());
idx++;
}
return pnodes[0];
}
void travel(haffman_node_s *root)
{
std::queue<haffman_node_s *> Q;
if (root)
{
Q.push(root);
}
FILE *pf = fopen("hfm.dot", "w");
fprintf(pf, "graph hfm {\n");
fprintf(pf, "\tgraph [ordering=\"out\"];\n");
while (!Q.empty())
{
haffman_node_s *node = Q.front();
Q.pop();
if (node->left)
{
fprintf(pf, "\t%c -- %c[color=\"red\", label=\"%d\"];\n", node->label, node->left->label, node->left->value);
Q.push(node->left);
}
if (node->right)
{
fprintf(pf, "\t%c -- %c[color=\"blue\", label=\"%d\"];\n", node->label, node->right->label, node->right->value);
Q.push(node->right);
}
}
fprintf(pf, "}\n");
fclose(pf);
system("dot hfm.dot -Tpng -o hfm.png");
}
void getCodeMap(haffman_node_s *root, std::unordered_map<char,std::string> & m, std::string & tmp)
{
if (!root)
{
return;
}
if (!root->left && !root->right)
{
m.insert(make_pair(root->label, tmp));
return;
}
if (root->left)
{
tmp.push_back(‘0‘);
getCodeMap(root->left, m, tmp);
tmp.pop_back();
}
if (root->right)
{
tmp.push_back(‘1‘);
getCodeMap(root->right, m, tmp);
tmp.pop_back();
}
}
void encode(const std::unordered_map<char,std::string> & m, const std::string & src, std::string & res)
{
for (char e : src)
{
res.append(m.at(e));
}
}
void decode(const std::unordered_map<char,std::string> & m, const std::string & src, std::string & res)
{
std::unordered_map<std::string, char> code;
for (auto e : m)
{
code.emplace(e.second, e.first);
}
for (auto e : code)
{
std::cout << e.first << ‘ ‘ << e.second << std::endl;
}
int srclen = src.size();
for (int idx = 0; idx < srclen; )
{
for (int i = 1; i <= srclen-idx; i++)
{
if (code.find(src.substr(idx, i)) != code.end())
{
res.push_back(code.at(src.substr(idx, i)));
idx += i;
break;
}
}
}
}
int main()
{
std::vector<char> label {‘A‘, ‘B‘, ‘C‘, ‘D‘, ‘E‘, ‘F‘};
std::vector<int> v {27, 8, 15, 15, 30, 5};
haffman_node_s *root = create_haffman_tree(label, v);
std::unordered_map<char,std::string> m;
std::string tmp;
getCodeMap(root, m, tmp);
for (auto e : m)
{
std::cout << e.first << ‘ ‘ << e.second << std::endl;
}
std::string src = "BADCADFEED";
std::string codestr;
encode(m, src, codestr);
std::cout << codestr << std::endl;
std::string decodestr;
decode(m, codestr, decodestr);
std::cout << decodestr << std::endl;
return 0;
}
原文:https://www.cnblogs.com/zuofaqi/p/10291563.html