看到题解大部分都是用‘递归+路径压缩’做的,所以本蒟蒻就来发一篇‘循环+路径压缩版并查集’的题解。速度比递归版本更加优秀(其实循环代码还要好写一些)。
并查集的操作有三步,初始化查找祖先与合并。
既然并查集是来查找祖先的,那么初始化就必然是让每个点的祖先指向自己
for(int i=1;i<=n;++i) fa[i]=i;查找操作就是不断地向上走,直到找到祖先为止
while(x!=fa[x]) x=fa[x];合并操作就是把一个节点的祖先变为另一个节点的祖先。
fa[find(a)]=find(b);//其中find(x)为x的祖先并查集的单次查询理想复杂度应该是O(logn)的,但是如果有一个这样的数据,并查集的复杂度就是O(n)了
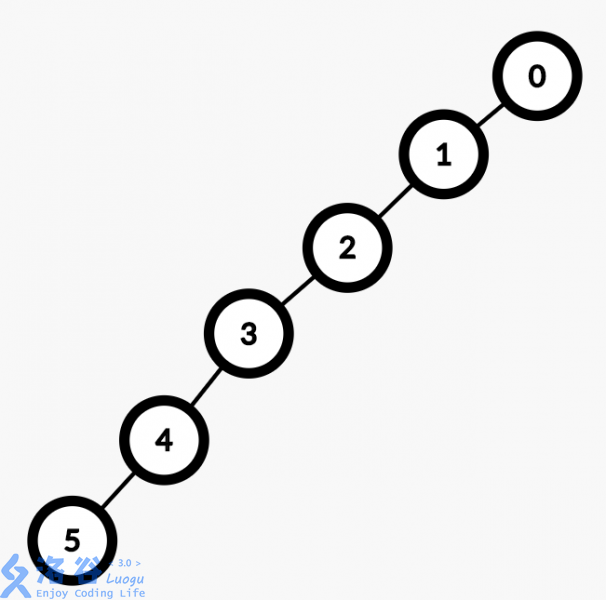
为了避免这种情况,我们需对路径进行压缩。
即当我们经过找到祖先节点后,回溯的时候顺便将它的子孙节点都直接指向祖先,使以后的查找复杂度变回O(logn)甚至更低,让图变成这样:
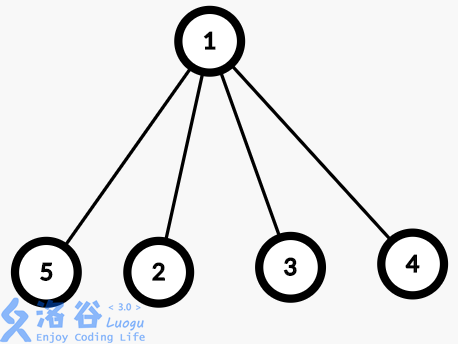
听上去十分高端,实际上只要把刚刚的查询操作变成如下就可以了
while(x!=fa[x]) x=fa[x]=fa[fa[x]];并查集有两个操作,既然查找可以优化,那合并可不可以呢?
我们可以进行按秩合并,即:合并的时候将元素少的集合合并到元素多的集合中,这样树高会小很多
附上代码:
#include <bits/stdc++.h>
using namespace std;
int n,m,z,x,y,fa[10005];//fa[i]是第i号节点的祖先
inline int find(int x)
{
while(x!=fa[x]) x=fa[x]=fa[fa[x]];
//让x和x的父亲变成他的父亲的父亲
//直到找到祖先才结束循环(x==fa[x])就意味着找到爹了
return x;
}
//循环版找爹函数
/*
//再附上递归版本的找爹函数
inline int find(int x)
{
if (x==fa[x]) return x;
//不停的递归查找
return fa[x]=find(fa[x]);
//路径压缩,可以缩短时间
}
*/
int main()
{
cin>>n>>m;
for(int i=1;i<=n;++i)
{
fa[i]=i;
//并查集的初始化
}
while(m--)
{
cin>>z>>x>>y;
int a=find(x),b=find(y);
//ab分别去找自己的爹
if(z==1)
{
fa[a]=b;
//并查集的合并操作,及将x点祖先的爹记为y点的祖先
}
if(z==2)
{
if(a==b)
{
puts("Y");
//爹一样就说明X与Y是在同一集合内,输出Y
}
else
{
puts("N");
//否则就说明X与Y是在同一集合内,输出N
}
}
}
return 0;
}原文:https://www.cnblogs.com/bcoier/p/10293079.html