Let C be an M × N matrix with real-valued entries, i.e. C={cij}mxn
Determinant is a value that can be computed from the elements of a square matrix. The determinant of a matrix A is denoted det(A), det A, or |A|.
In the case of a 2 × 2 matrix the determinant may be defined as:

Similarly, for a 3 × 3 matrix A, its determinant is:

See more information about determinant here.
The Rank of a matrix is the number of linearly independent rows (or columns) in it, so rank(C)≤min(m,n).
A common approach to finding the rank of a matrix is to reduce it to a simpler form, generally row echelon form, by elementary row operations. The rank equals to the number of non-zero rows of the final matrix (in row echelon form).
The reduce step can be found in this article.
For a square M × M matrix C and a vector x that is not all zeros, the values of λ satisfying
![]()
are called the eigenvalues of C . The N-vector ?x satisfying the equation above for an eigenvalue λ is the corresponding right eigenvector.
The eigenvalues of C are then the solutions of
|(C ? λIM)| = 0,
where |S| denotes the determinant of a square matrix S.
For each value of λ, we can calculate the corresponding eigenvector x through solving the following equation:
![]()
This article gives a specific example of the calculating process.
Let S be a square real-valued M × M matrix with M linearly independent eigenvectors. Then there exists an eigen decomposition
![]()
where the columns of U are the eigenvectors of S and Λ is a diagonal matrix whose diagonal entries are the eigenvalues of S in decreasing order
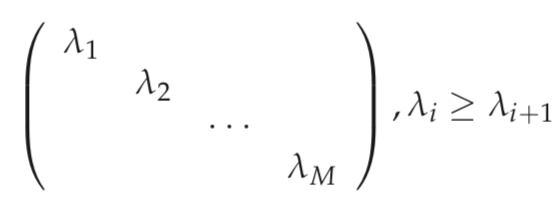
If the eigenvalues are distinct, then this decomposition is unique.
Let S be a square, symmetric real-valued M × M matrix with M linearly independent eigenvectors. Then there exists a symmetric diagonal decomposition
S = QΛQT
where the columns of Q are the orthogonal and normalized (unit length, real) eigenvectors of S, and Λ is the diagonal matrix whose entries are the eigenvalues of S.
Further, all entries of Q are real and we have Q?1 = QT.
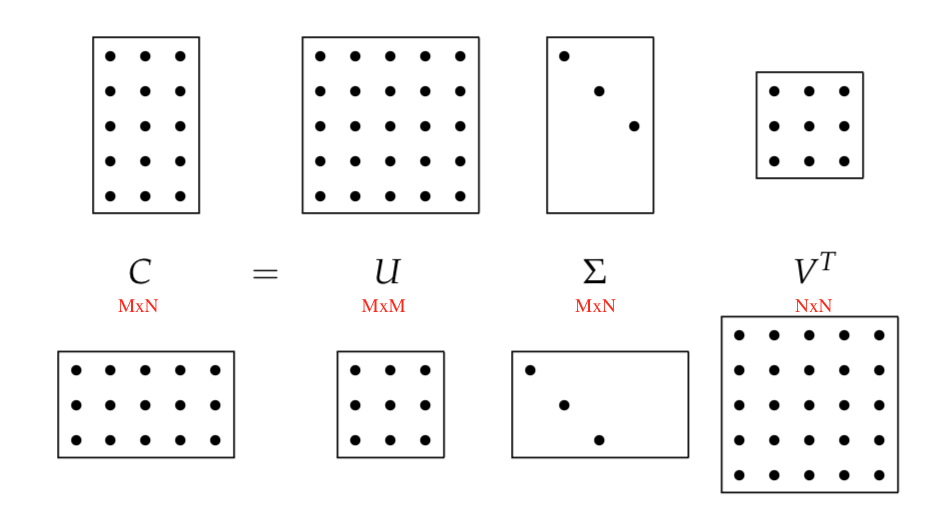
Let r be the rank of the M × N matrix C. Then, there is a singular- value decomposition (SVD for short) of C of the form
![]()
where
1. U is the M × M matrix whose columns are the orthogonal eigenvectors of CCT.
2. V is the N × N matrix whose columns are the orthogonal eigenvectors of CTC.
3. 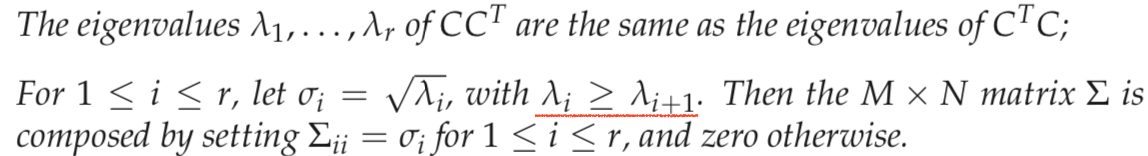
The values σi are referred to as the singular values of C.
Here is the illustration of the singular-value decomposition.
[Math Review] Linear Algebra for Singular Value Decomposition (SVD)
原文:https://www.cnblogs.com/sherrydatascience/p/10293948.html