A - Bone Collector HDU - 2602
题意:给定背包的最大体积和物品的数量,每一个物品的价值和体积,01背包板子
题解:01背包

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<sstream> #include<cmath> #include<stack> #include<cstdlib> #include <vector> #include<queue> using namespace std; #define ll long long #define llu unsigned long long #define INF 0x3f3f3f3f #define PI acos(-1.0) const int maxn = 1e5+5; const int mod = 1e9+7; ll value[maxn]; ll weight[maxn]; ll dp[maxn]; void init() { memset(value,0,sizeof value); memset(weight,0,sizeof weight); memset(dp,0,sizeof dp); } int main() { int t; scanf("%d",&t); while(t--) { init(); ll N,V; scanf("%lld %lld",&N,&V); for(int i = 1; i <= N; i++) scanf("%lld",&value[i]); for(int i = 1; i <= N; i++) scanf("%lld",&weight[i]); for(int i = 1; i <= N; i++) for (int j = V; j >= weight[i]; j--) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); printf("%lld\n",dp[V]); } }
B - 饭卡 HDU - 2546
电子科大本部食堂的饭卡有一种很诡异的设计,即在购买之前判断余额。如果购买一个商品之前,卡上的剩余金额大于或等于5元,就一定可以购买成功(即使购买后卡上余额为负),否则无法购买(即使金额足够)。所以大家都希望尽量使卡上的余额最少。
某天,食堂中有n种菜出售,每种菜可购买一次。已知每种菜的价格以及卡上的余额,问最少可使卡上的余额为多少。
Input多组数据。对于每组数据:
第一行为正整数n,表示菜的数量。n<=1000。
第二行包括n个正整数,表示每种菜的价格。价格不超过50。
第三行包括一个正整数m,表示卡上的余额。m<=1000。
n=0表示数据结束。
Output对于每组输入,输出一行,包含一个整数,表示卡上可能的最小余额。Sample Input
1 50 5 10 1 2 3 2 1 1 2 3 2 1 50 0
Sample Output
-45 32
思路:动态规划,最后一次肯定是买最贵的那个菜,之前就余额大于等于5的前提下,能买多少就买多少

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<sstream> #include<cmath> #include<stack> #include<cstdlib> #include <vector> #include<queue> using namespace std; #define ll long long #define llu unsigned long long #define INF 0x3f3f3f3f #define PI acos(-1.0) const int maxn = 1e5+5; const int mod = 1e9+7; ll value[maxn]; ll weight[maxn]; ll dp[maxn]; void init() { memset(value,0,sizeof value); memset(weight,0,sizeof weight); memset(dp,0,sizeof dp); } int main() { while(true) { init(); ll N,V; scanf("%lld",&N); if(N == 0) break; // for(int i = 1; i <= N; i++) // scanf("%lld",&value[i]); ll maxx = -1; ll pos; for(int i = 1; i <= N; i++) { scanf("%lld", &weight[i]); if(maxx < weight[i]) { maxx = weight[i]; pos = i; } } scanf("%lld",&V); if(V < 5) { printf("%lld\n", V); continue; } for(int i = 1; i <= N; i++) { if(i == pos) continue; for (int j = V; j >= weight[i]; j--) { dp[j] = max(dp[j], dp[j - weight[i]] + weight[i]); } } printf("%lld\n",V - dp[V-5] - maxx); } }
C - 湫湫系列故事——减肥记I HDU - 4508
Input 输入包含多组测试用例。
每组数据以一个整数n开始,表示每天的食物清单有n种食物。
接下来n行,每行两个整数a和b,其中a表示这种食物可以带给湫湫的幸福值(数值越大,越幸福),b表示湫湫吃这种食物会吸收的卡路里量。
最后是一个整数m,表示湫湫一天吸收的卡路里不能超过m。
[Technical Specification]
1. 1 <= n <= 100
2. 0 <= a,b <= 100000
3. 1 <= m <= 100000
Output 对每份清单,输出一个整数,即满足卡路里吸收量的同时,湫湫可获得的最大幸福值。Sample Input
3 3 3 7 7 9 9 10 5 1 1 5 3 10 3 6 8 7 5 6
Sample Output
10 20
题解:完全背包

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<sstream> #include<cmath> #include<stack> #include<cstdlib> #include <vector> #include<queue> using namespace std; #define ll long long #define llu unsigned long long #define INF 0x3f3f3f3f #define PI acos(-1.0) const int maxn = 1e5+5; const int mod = 1e9+7; ll value[maxn]; ll weight[maxn]; ll dp[maxn]; void init() { memset(value,0,sizeof value); memset(weight,0,sizeof weight); memset(dp,0,sizeof dp); } int main() { ll N,V; while(~scanf("%lld",&N)) { init(); for (int i = 1; i <= N; i++) { scanf("%lld %lld", &value[i], &weight[i]); } scanf("%lld", &V); for (int i = 1; i <= N; i++) for (int j = weight[i]; j <= V; j++) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); printf("%lld\n", dp[V]); } }
D - 寒冰王座 HDU - 1248
Input输入数据的第一行是一个整数T(1<=T<=100),代表测试数据的数量.然后是T行测试数据,每个测试数据只包含一个正整数N(1<=N<=10000),N代表死亡骑士手中钞票的面值.
注意:地精商店只有题中描述的三种道具.
题解:物品的value和weight已知

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<sstream> #include<cmath> #include<stack> #include<cstdlib> #include <vector> #include<queue> using namespace std; #define ll long long #define llu unsigned long long #define INF 0x3f3f3f3f #define PI acos(-1.0) const int maxn = 1e5+5; const int mod = 1e9+7; ll value[maxn]={150,200,350}; ll weight[maxn]={150,200,350}; ll dp[maxn]; void init() { // memset(value,0,sizeof value); // memset(weight,0,sizeof weight); memset(dp,0,sizeof dp); } int main() { ll N,V; int t; scanf("%d",&t); while(t--) { //scanf("%lld",&N); init(); // for (int i = 1; i <= N; i++) { // scanf("%lld %lld", &value[i], &weight[i]); // } scanf("%lld", &V); for (int i = 0; i <= 2; i++) for (int j = weight[i]; j <= V; j++) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); printf("%lld\n", V - dp[V]); } }
E - Course Selection System ZOJ - 3956
题意:有 n 门课程,每门课程都有它的快乐值 Hi,学分 Ci。现在选择若干门课程(可不选),它们的舒适值的结果满足下式:
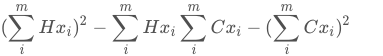
求舒适值最大是多少
题解:难点在于题目的理解,理解题目的意思并找到题目的每门课的value是H,weight是C

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<sstream> #include<cmath> #include<stack> #include<cstdlib> #include <vector> #include<queue> using namespace std; #define ll long long #define llu unsigned long long #define INF 0x3f3f3f3f #define PI acos(-1.0) const int maxn = 1e5+5; const int mod = 1e9+7; ll value[maxn]; ll weight[maxn]; ll dp[maxn]; ll calculate(ll C ,ll H) { return H*H - H*C -C*C; } void init() { memset(value,0,sizeof value); memset(weight,0,sizeof weight); memset(dp,0,sizeof dp); } int main() { int t; scanf("%d",&t); while(t--) { init(); ll N,V = 0; ll ans = 0; scanf("%lld",&N); for(int i = 1; i <= N; i++) { scanf("%lld %lld", &value[i], &weight[i]); V += weight[i]; } for(int i = 1; i <= N; i++) for (int j = V; j >= weight[i]; j--) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); for(int i = 0;i <= V;i++) ans = max(ans,calculate(i,dp[i])); printf("%lld\n",ans); } }
F - 悼念512汶川大地震遇难同胞——珍惜现在,感恩生活 HDU - 2191
中文题题意跳过了
思路:多重背包问题。可以转换成为01背包解。多重背包转化为01背包的关键在于把件数从整体中孤立出来作为一个新的个体,也就是说不管分类,有多少件就有多少种
01做法:

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<sstream> #include<cmath> #include<stack> #include<cstdlib> #include <vector> #include<queue> using namespace std; #define ll long long #define llu unsigned long long #define INF 0x3f3f3f3f #define PI acos(-1.0) const int maxn = 1e5+5; const int mod = 1e9+7; ll value[maxn]; ll weight[maxn]; ll dp[maxn]; void init() { memset(value,0,sizeof value); memset(weight,0,sizeof weight); memset(dp,0,sizeof dp); } int main() { int t; scanf("%d",&t); while(t--) { init(); ll V,m; scanf("%lld %lld",&V,&m); int N = 1; for(int i=1;i<=m;i++) { int a,b,c; scanf("%d%d%d",&a,&b,&c); for(int j=1;j<=c;j++) { weight[N] = a; value[N] = b; N++; } } for(int i = 1; i <=N; i++) for (int j = V; j >= weight[i]; j--) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); printf("%lld\n",dp[V]); } }
多重做法:

#include<cstdio> #include<cstring> #include<iostream> using namespace std; const int maxn=500; int n,m,w[maxn],c[maxn],num[maxn],dp[maxn]; int main() { int T; scanf("%d",&T); while(T--) { int cur=0; scanf("%d%d",&n,&m); for(int i=0;i<m;i++) scanf("%d%d%d",&w[i],&c[i],&num[i]); int ans=0; memset(dp,0,sizeof(dp)); for(int i=0;i<m;i++) { for(int j=n;j>=w[i];j--) { for(int k=1;k<=num[i];k++) if(j>=k*w[i]) dp[j]=max(dp[j],dp[j-k*w[i]]+c[i]*k); ans=max(ans,dp[j]); } } printf("%d\n",ans); } return 0; }
G - ACboy needs your help HDU - 1712
题意:题意是有N天要学M门课,A[i][j]表示第i门课要上j天才可以获得的价值,每天最多只能上一门课,求N天可以获得的最大价值。
题解:难点在于题意,题意明白之后可知输入的是value[i][j],其中i是第i门课,j是需要花费j天,value[i][j]是第i门课话费j天可以获得的价值,每一门课不可以重复学习只能选择花费某天就可以理解为这一组里面只能选一个

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> #include<sstream> #include<cmath> #include<stack> #include<cstdlib> #include <vector> #include<queue> using namespace std; #define ll long long #define llu unsigned long long #define INF 0x3f3f3f3f #define PI acos(-1.0) const int maxn = 1e2+5; const int mod = 1e9+7; ll value[maxn][maxn]; ll weight[maxn]; ll dp[maxn]; ll a[maxn][maxn]; void init() { memset(value,0,sizeof value); memset(weight,0,sizeof weight); memset(dp,0,sizeof dp); } int main() { // int t; // scanf("%d",&t); ll n; ll N,V; while(~scanf("%lld %lld",&n,&V) && n+V) { init(); for(int i=1;i<=n;i++) { for (int j = 1; j <= V; j++) { scanf("%d", &value[i][j]); } } for(int i = 1; i <= n; i++) //第一个循环枚举第几组(这里是第几个课程) for (int j = V; j >= 0; j--) //第二个循环枚举背包的容量 for(int k = 1; k <= j; k++) //第三个循环枚举该组里的物品(这里是第i门课花费的1~j天) dp[j] = max(dp[j], dp[j - k] + value[i][k]); printf("%lld\n",dp[V]); } }
原文:https://www.cnblogs.com/smallhester/p/10296395.html