用途:分类预处理中的降维,做分类任务
目的:LDA关心的是能够最大化类间区分度的坐标轴
将特征空间(数据中的多维样本,将投影到一个维度更小的K维空间,保持区别类型的信息)
监督性:LDA是“有监督”的,它计算的是另一个类特定的方向
投影:找到更适用的分类空间
与PCA不同: 更关心分类而不是方差(PCA更关心的是方差)

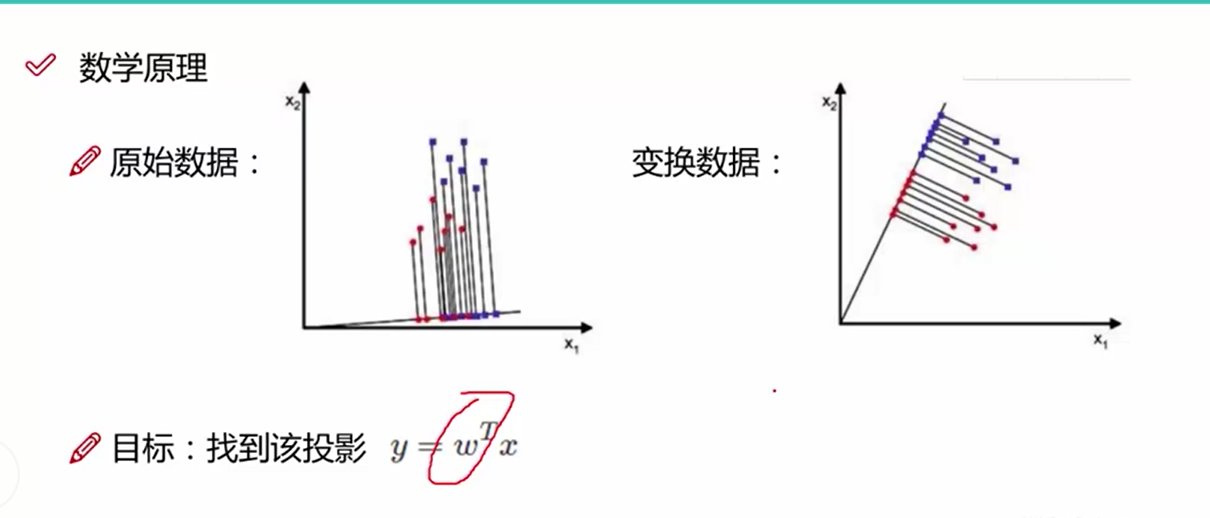
如图所示,找到合适的方向投影后的数据更加的分散
LDA的数据原理:
目标找到投影:y = w^T * x ,我们需要求解出w
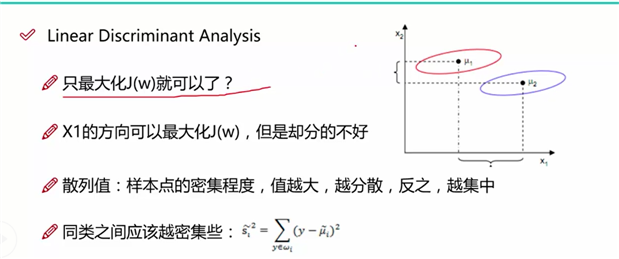
LDA的第一个目标是使得投影后两个类别之间的距离越大越好,使用的判别依据,是投影后两个类别的中心点的距离越大越好,即均值u1^ - u2^
第一步:求出当前均值和投影后的均值
J(W) = |w^T(u1 - u2)| # 计算投影以后的两个类别中心位置之差

LDA的第二个目标是使得投影后的类别之间的距离越来越小,从图一中我们可以看出,只讨论类别之间的距离是不够的, 同类之间的距离使用单个类别的数据到类别中心之差来表示,值越大,同类数据越分散,值越小,同类数据越集中,我们需要使得这个值的大小越小越好
根据上面两个目标函数,我们做一个组合, 分子使用类间距离, 分母使用类内距离,求得组合后的最大值

该图表示的是最终的目标函数(类间距离/类内距离),这里的类内散布矩阵:通过同种类别数据-该类别的均值之差进行加和后求得
求得类间距离的散步矩阵

上述的目标矩阵就是我们求解的方程,我们需要求得其最大值
构造拉格朗日方程, 我们对分母进行缩放,使得w^TSw*w = 1, 作为限制条件
cw = w^T*SB*w - a(w^T*Sw*w-1) --构造的拉格朗日方程
cw/dw = w^T*SB*w - a(w^T*Sw*w-1) / dw 对上述方程使用dw进行求导,求偏导等于零求最大值
2SB*w - 2*a*Sw * w = 0
a * w = Sw^-1*SB*w ---- a*w = A*w
w是Sw^-1*SB的特征向量

原文:https://www.cnblogs.com/my-love-is-python/p/10301605.html