一、电商RFM模型
RFM模型是一个简单的根据客户的活跃程度和交易金额贡献所做的分类。因为操作简单,所以较为常用。
近度R:R代表客户最近的活跃时间距离数据采集点的时间距离,R越大,表示客户越久未发生交易,R越小,表示客户越近有交易发生。R越大则客户越可能会“沉睡”,流失的可能性越大。在这部分客户中,可能有些优质客户,值得公司通过一定的营销手段进行激活。
频度F:F代表客户过去某段时间内的活跃频率。F越大,则表示客户同本公司的交易越频繁,不仅仅给公司带来人气,也带来稳定的现金流,是非常忠诚的客户;F越小,则表示客户不够活跃,且可能是竞争对手的常客。针对F较小、且消费额较大的客户,需要推出一定的竞争策略,将这批客户从竞争对手中争取过来。
额度M:表示客户每次消费金额的多少,可以用最近一次消费金额,也可以用过去的平均消费金额,根据分析的目的不同,可以有不同的标识方法。一般来讲,单次交易金额较大的客户,支付能力强,价格敏感度低,是较为优质的客户,而每次交易金额很小的客户,可能在支付能力和支付意愿上较低。当然,也不是绝对的。
通过RFM分析将客户群体划分成一般保持客户、一般发展客户、一般价值客户、一般挽留客户、重要保持客户、重要发展客户、重要价值客户、要挽留客户等八个级别。
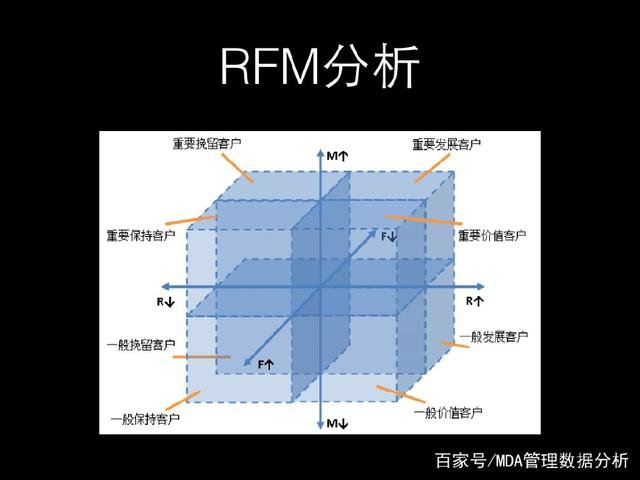
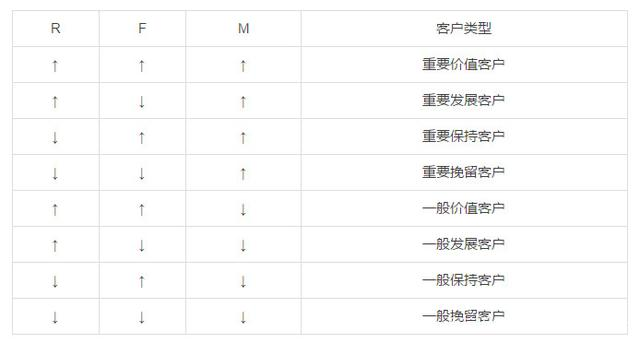
对于传统RFM模型,根据3个指标,划分8个客群,进行精细化运营、营销、管理。
二、MRC模型
根据RFM模型,整理线下支付机构最关注的指标,发现频次意义较小,线下支付机构主要靠商户端的套现手续费盈利。保留R、M,新增C指标,定义为笔均x贷记卡笔数占比。
从取数,到统计展示,做简单的过程梳理、记录。
1、取数
---支付机构MRC模型 select t1.pos_sn, t1.amt 总交易量, ceil(sysdate - t1.maxday) 最后交易距今天数, trunc((t1.amt/t1.cot)*(t1.credcot/t1.cot),0) 笔均x贷记卡笔占比, t1.cot 笔数, trunc(t1.amt/t1.cot,0) 笔均, t1.credcot 贷记卡笔数, trunc(t1.credcot/t1.cot,3) 贷记卡笔数占比, p.agent_no 所属代理 from (select ptd.pos_sn,max(ptd.order_time) maxday,sum(ptd.trans_amount) amt, sum(ptd.trans_num) cot, sum(case when ptd.card_type in (‘CREDIT_CARD‘,‘SEMI_CREDIT_CARD‘) then ptd.trans_num else 0 end) credcot from posp_boss.pos_trans_day ptd group by ptd.pos_sn)t1 left join posp_boss.pos p on p.pos_sn = t1.pos_sn where p.deposit_flg = 1 ---and pos.type = ‘MF90‘ order by t1.amt desc,ceil(sysdate - t1.maxday)
使用Oracle数据库,已有按聚合的机具日交易量表,取出关键指标。

2、分析
由于数据量超过40万,用EXCEL分析较为卡顿,使用python 进行统计展示。
总交易量 最后交易距今天数 笔均X贷记卡笔占比 count 4.241090e+05 424109.000000 424109.000000 mean 5.513364e+05 46.862840 5105.828933 std 1.013319e+06 65.365966 4705.183574 min 1.000000e-02 2.000000 0.000000 25% 4.020922e+04 4.000000 1782.000000 50% 2.099190e+05 13.000000 3864.000000 75% 6.919676e+05 68.000000 7015.000000 max 4.194847e+07 372.000000 95453.000000
用简单的K均值聚类尝试分群
import pandas as pd import numpy as np from sklearn.cluster import KMeans mrc = pd.read_csv("C:/Users/wangd/Desktop/MRC.csv") mrc.head() mrc.iloc[:,1:4].describe() #转化为数组 km = np.array(mrc.iloc[:,1:4]) #设置随机数 seed=9 #对数据进行聚类 clf=KMeans(n_clusters=8,random_state=seed) #拟合模型 clf=clf.fit(km) #查看聚类质心点 clf.cluster_centers_ #对原数据表进行类别标记 mrc[‘label‘]= clf.labels_ #查看标记后的数据 mrc.head() #计算每个类别的数据量 c=mrc["label"].value_counts()
array([[8.23851049e+04, 5.19385405e+01, 3.62929498e+03], [3.57622006e+06, 5.53870694e+01, 7.05173435e+03], [1.08953507e+06, 4.87523004e+01, 7.16840196e+03], [1.04298146e+07, 6.42577938e+01, 5.69444724e+03], [2.02866108e+06, 4.90190455e+01, 7.49004477e+03], [4.96078891e+05, 3.00557403e+01, 6.84247185e+03], [1.97803666e+07, 6.25615385e+01, 6.66596154e+03], [6.13333712e+06, 6.27500000e+01, 6.26144459e+03]])
0 239447
5 89931
2 60533
4 22023
1 8250
7 2961
3 834
6 130
Name: label, dtype: int64
分类效果解读稍繁琐,也需要交叉验证。接下来尝试传统的三分法。
原文:https://www.cnblogs.com/daoren/p/10311131.html