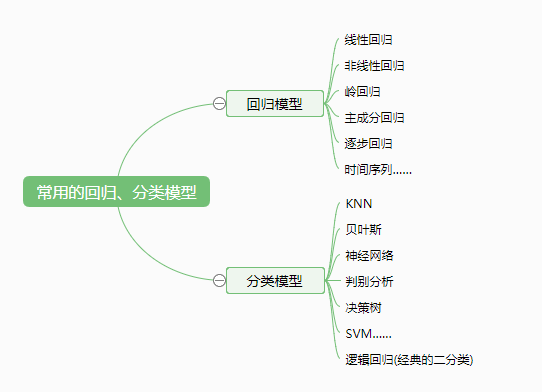
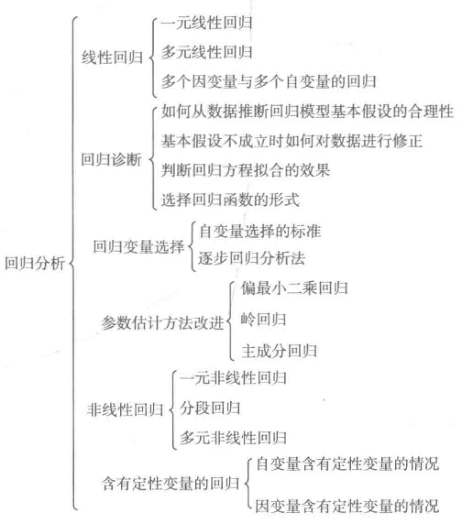
回归分析研究的范围大致如下:
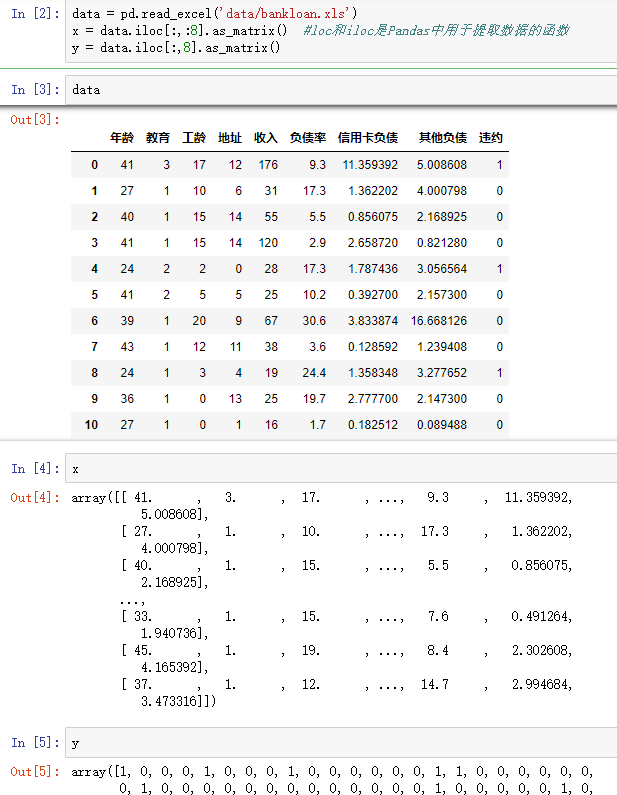

#逻辑回归 自动建模 import pandas as pd from sklearn.linear_model import LogisticRegression as LR from sklearn.linear_model import RandomizedLogisticRegression as RLR #参数初始化 data = pd.read_excel(‘data/bankloan.xls‘) x = data.iloc[:,:8].as_matrix() #loc和iloc是Pandas中用于提取数据的函数 y = data.iloc[:,8].as_matrix() #复制一份,用作对比 x1=x y1=y rlr = RLR() #建立随机逻辑回归模型,筛选变量 rlr.fit(x, y) #训练模型 rlr.get_support() #获取特征筛选结果,也可以通过.scores_方法获取各个特征的分数 print(u‘通过随机逻辑回归模型筛选特征结束。‘) print(u‘有效特征为:%s‘ % ‘,‘.join(data.iloc[:,0:8].columns[rlr.get_support()])) #原代码此处报错 x = data[data.iloc[:,0:8].columns[rlr.get_support()]].as_matrix() #筛选好特征 lr = LR() #建立逻辑回归模型 lr.fit(x, y) #用筛选后的特征数据来训练模型 print(u‘逻辑回归模型训练结束。‘) print(u‘筛选特征后,模型的平均正确率为:%s‘ % lr.score(x, y)) #给出模型的平均正确率,本例为81.4% lr1 = LR() lr1.fit(x1, y1) #直接用原始数据来训练模型 print(u‘未筛选特征,模型的平均正确率为:%s‘ % lr1.score(x1, y1))
通过随机逻辑回归模型筛选特征结束。 有效特征为:工龄,地址,负债率,信用卡负债 逻辑回归模型训练结束。 筛选特征后,模型的平均正确率为:0.814285714286 未筛选特征,模型的平均正确率为:0.805714285714
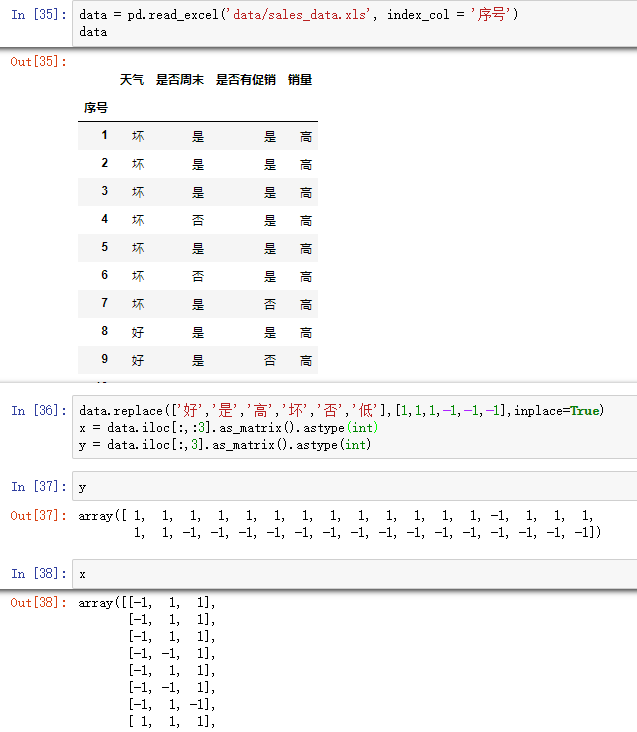
#使用ID3决策树算法预测销量高低 import pandas as pd #参数初始化 data = pd.read_excel(‘data/sales_data.xls‘, index_col = ‘序号‘) #导入数据 #数据是类别标签,要将它转换为数据 #用1来表示“好”、“是”、“高”这三个属性,用-1来表示“坏”、“否”、“低” data.replace([‘好‘,‘是‘,‘高‘,‘坏‘,‘否‘,‘低‘],[1,1,1,-1,-1,-1],inplace=True) x = data.iloc[:,:3] y = data.iloc[:,3] from sklearn.tree import DecisionTreeClassifier as DTC dtc = DTC(criterion=‘entropy‘) #建立决策树模型,基于信息熵 dtc.fit(x, y) #训练模型 #导入相关函数,可视化决策树。 #导出的结果是一个dot文件,需要安装Graphviz才能将它转换为pdf或png等格式。 from sklearn.tree import export_graphviz x = pd.DataFrame(x) from sklearn.externals.six import StringIO x = pd.DataFrame(x) with open("tree.dot", ‘w‘) as f: f = export_graphviz(dtc, feature_names = x.columns, out_file = f)
运行上述代码,生成tree.dot文件,对其稍作修改
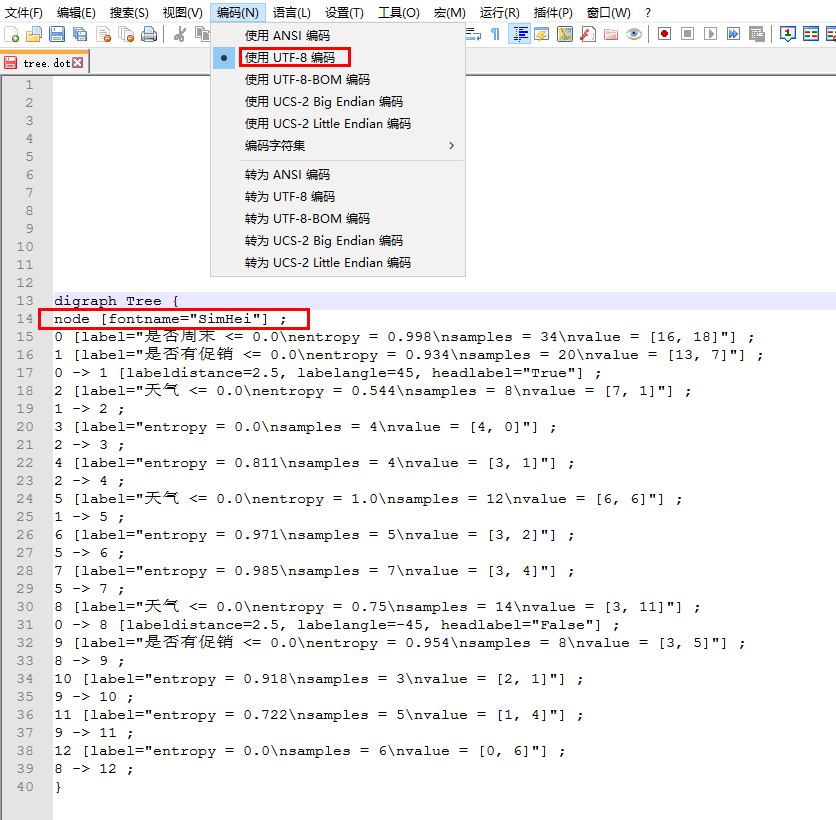
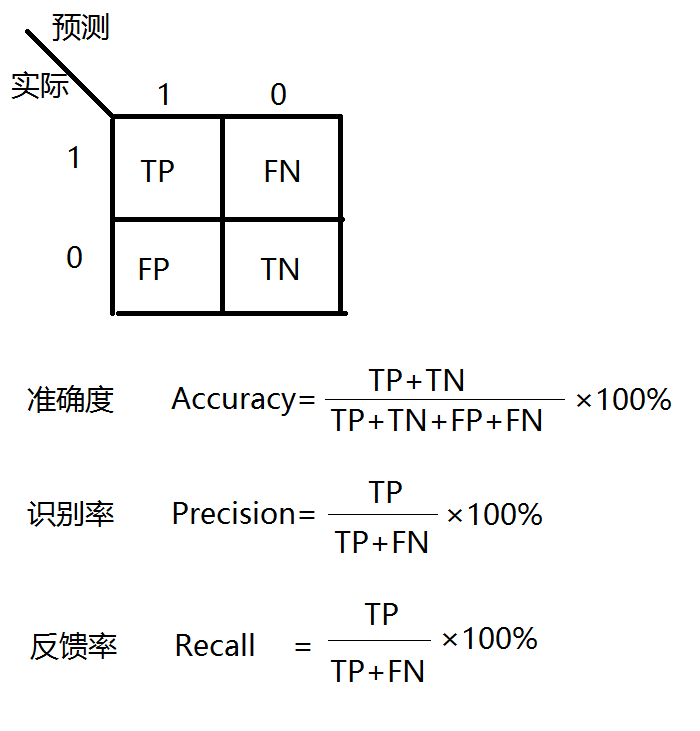
得到决策树的可视化
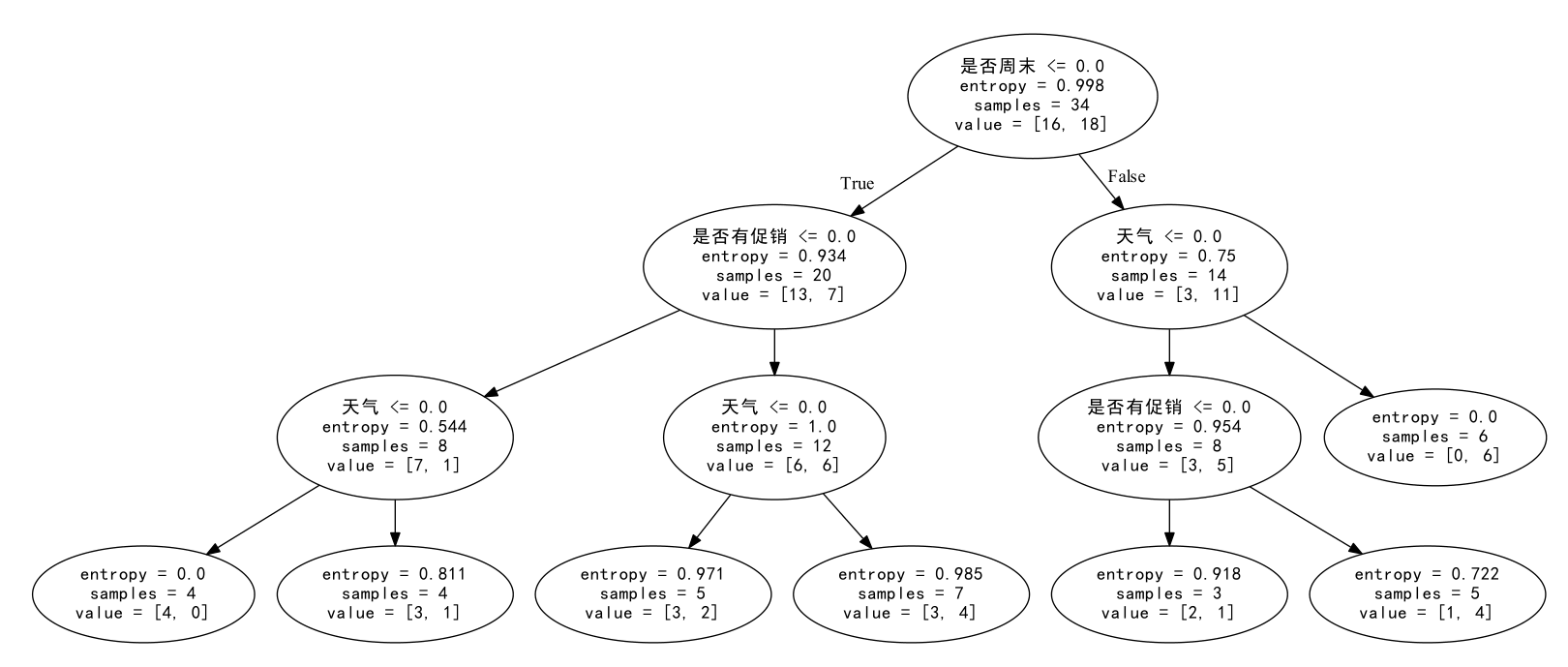
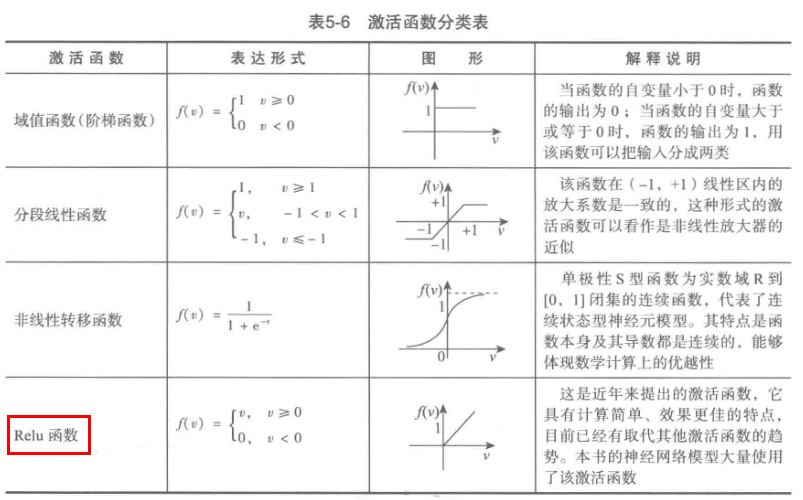


#使用神经网络算法预测销量高低 import pandas as pd from sklearn.metrics import confusion_matrix #导入混淆矩阵函数 import matplotlib.pyplot as plt #导入作图库 from keras.models import Sequential from keras.layers.core import Dense, Activation #作图函数 def cm_plot(y, yp): cm = confusion_matrix(y, yp) #混淆矩阵 plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图,配色风格使用cm.Greens,更多风格请参考官网。 plt.colorbar() #颜色标签 for x in range(len(cm)): #数据标签 for y in range(len(cm)): plt.annotate(cm[x,y], xy=(x, y), horizontalalignment=‘center‘, verticalalignment=‘center‘) plt.ylabel(‘True label‘) #坐标轴标签 plt.xlabel(‘Predicted label‘) #坐标轴标签 return plt #参数初始化 data = pd.read_excel(‘data/sales_data.xls‘, index_col = ‘序号‘) #导入数据 #数据是类别标签,要将它转换为数据 #用1来表示“好”、“是”、“高”这三个属性,用0来表示“坏”、“否”、“低” data.replace([‘好‘,‘是‘,‘高‘,‘坏‘,‘否‘,‘低‘],[1,1,1,0,0,0],inplace=True) x = data.iloc[:,:3] y = data.iloc[:,3] model = Sequential() #建立模型 model.add(Dense(input_dim = 3, output_dim = 10)) model.add(Activation(‘relu‘)) #用relu函数作为激活函数,能够大幅提供准确度 model.add(Dense(input_dim = 10, output_dim = 1)) model.add(Activation(‘sigmoid‘)) #由于是0-1输出,用sigmoid函数作为激活函数 model.compile(loss = ‘binary_crossentropy‘, optimizer = ‘adam‘) #编译模型。由于我们做的是二元分类,所以我们指定损失函数为binary_crossentropy,以及模式为binary #另外常见的损失函数还有mean_squared_error、categorical_crossentropy等,请阅读帮助文件。 #求解方法我们指定用adam,还有sgd、rmsprop等可选 model.fit(x, y, nb_epoch = 1000, batch_size = 10) #训练模型,学习一千次 yp = model.predict_classes(x).reshape(len(y)) #分类预测 cm_plot(y,yp).show() #显示混淆矩阵可视化结果
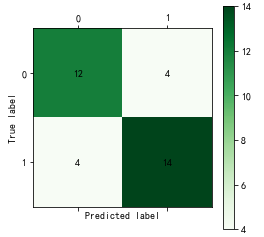


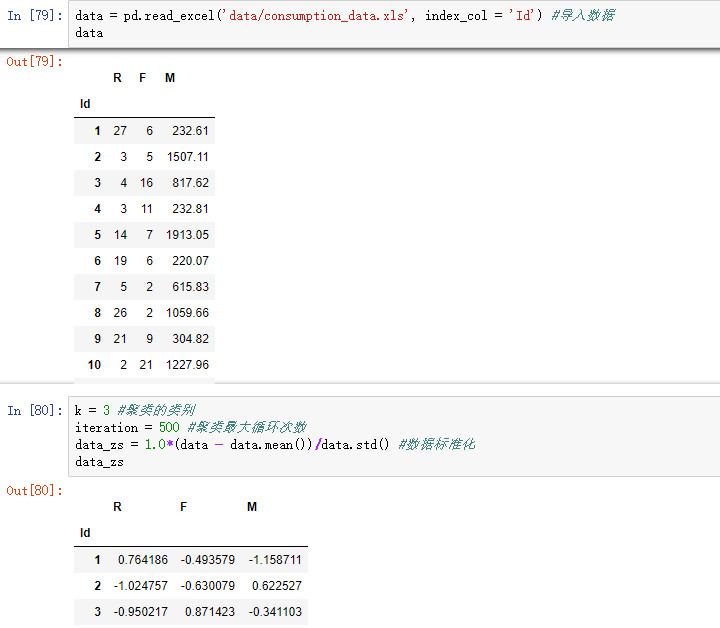
#-*- coding: utf-8 -*- #使用K-Means算法聚类消费行为特征数据 import pandas as pd import matplotlib.pyplot as plt from sklearn.cluster import KMeans #参数初始化 data = pd.read_excel(‘data/consumption_data.xls‘, index_col = ‘Id‘) #读取数据 outputfile = ‘tmp/data_type.xls‘ #保存结果的文件名 k = 3 #聚类的类别 iteration = 500 #聚类最大循环次数 data_zs = 1.0*(data - data.mean())/data.std() #数据标准化 model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration) #分为k类,并发数4 model.fit(data_zs) #开始聚类 #简单打印结果 r1 = pd.Series(model.labels_).value_counts() #统计各个类别的数目 r2 = pd.DataFrame(model.cluster_centers_) #找出聚类中心 r = pd.concat([r2, r1], axis = 1) #横向连接(0是纵向),得到聚类中心对应的类别下的数目 r.columns = list(data.columns) + [u‘类别数目‘] #重命名表头 print(r) #详细输出原始数据及其类别 r = pd.concat([data, pd.Series(model.labels_, index = data.index)], axis = 1) #详细输出每个样本对应的类别 r.columns = list(data.columns) + [u‘聚类类别‘] #重命名表头 r.to_excel(outputfile) #保存结果 def density_plot(data,title): #自定义作图函数 plt.figure() for i in range(len(data.iloc[0])):#逐列作图 (data.iloc[:,i]).plot(kind=‘kde‘, label=data.columns[i],linewidth = 2) plt.ylabel(‘密度‘) plt.xlabel(‘人数‘) plt.title(‘聚类类别%s各属性的密度曲线‘%title) plt.legend() return plt def density_plot(data): #自定义作图函数 p = data.plot(kind=‘kde‘, linewidth = 2, subplots = True, sharex = False) [p[i].set_ylabel(u‘密度‘) for i in range(k)] plt.legend() return plt pic_output = ‘tmp/pd_‘ #概率密度图文件名前缀 for i in range(k): density_plot(data[r[u‘聚类类别‘]==i]).savefig(u‘%s%s.png‘ %(pic_output, i))

#代码接上面 from sklearn.manifold import TSNE tsne = TSNE() tsne.fit_transform(data_zs) #进行数据降维 tsne = pd.DataFrame(tsne.embedding_, index = data_zs.index) #转换数据格式 #不同类别用不同颜色和样式绘图 d = tsne[r[u‘聚类类别‘] == 0] plt.plot(d[0], d[1], ‘r.‘) d = tsne[r[u‘聚类类别‘] == 1] plt.plot(d[0], d[1], ‘go‘) d = tsne[r[u‘聚类类别‘] == 2] plt.plot(d[0], d[1], ‘b*‘) plt.show()
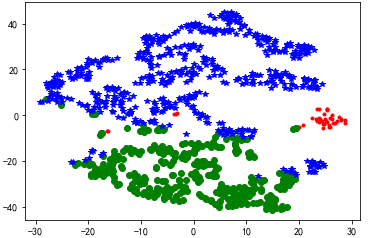
原文:https://www.cnblogs.com/little-monkey/p/10312045.html