一、简介
1. 定义
解释器模式(Interpreter),给定一个语言,定义它的文法的一种表示,并定义一个解释器,这个解释器使用该表示来解释语言中的句子。
2. 应用场景
本模式适用于处理运算式等字符串的解析操作。
3. 优点
提供灵活的表达式解析处理方式,通过封装的对外接口,调用者可以不再关心具体的表达式处理规则。
4. 缺点
使用递归编码,需要在实现过程中注意递归的返回条件。
二、类图
1. 设计模式类图
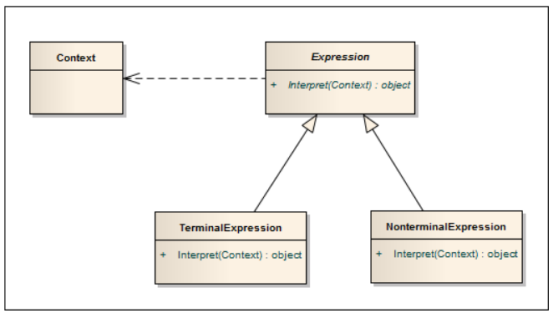
AbstractExpression:定义解释器的接口,约定解释器的解释操作。其中的Interpret接口,正如其名字那样,它是专门用来解释该解释器所要实现的功能。(如加法解释器中的Interpret接口就是完成两个操作数的相加功能)。
TerminalExpression:终结符解释器,用来实现语法规则中和终结符相关的操作,不再包含其他的解释器,如果用组合模式来构建抽象语法树的话,就相当于组合模式中的叶子对象,可以有多种终结符解释器。
NonterminalExpression:非终结符解释器,用来实现语法规则中非终结符相关的操作,通常一个解释器对应一个语法规则,可以包含其他解释器,如果用组合模式构建抽象语法树的话,就相当于组合模式中的组合对象。可以有多种非终结符解释器。
Context:上下文,通常包含各个解释器需要的数据或是公共的功能。这个Context在解释器模式中起着非常重要的作用。一般用来传递被所有解释器共享的数据,后面的解释器可以从这里获取这些值。
Client:客户端,指的是使用解释器的客户端,通常在这里将按照语言的语法做的表达式转换成使用解释器对象描述的抽象语法树,然后调用解释操作。
三、代码示例
1. 本文以运算式解析为例,类图如下:
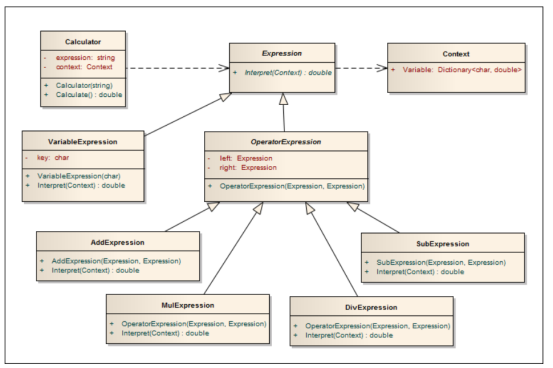
#ifndef INTERPRETER_H #define INTERPRETER_H #include <QDebug> #include <iostream> #include <QString> #include <QMap> #include <QStack> #include <typeinfo> class Expression { public: Expression() {}; virtual ~Expression() {}; /** * @brief : 解析公式和数值 * @param[in] : var key是公式中的参数,value值是具体的数字 * @return : int */ virtual int interpreter(QMap<QString, int>& var) = 0; }; class VarExpression : public Expression { public: VarExpression(QString key) : m_key(key) {}; ~VarExpression() {}; int interpreter(QMap<QString, int>& var) { return var[m_key]; } private: QString m_key; }; class SymbolExpression : public Expression { public: SymbolExpression(Expression* left, Expression* right) : m_left(left) , m_right(right) {}; Expression* getLeft() { return m_left; } Expression* getRight() { return m_right; } protected: Expression* m_left; Expression* m_right; }; //加法解析器 class AddExpression : public SymbolExpression { public: AddExpression(Expression* left, Expression* right) : SymbolExpression(left, right) {}; ~AddExpression() {}; int interpreter(QMap<QString, int>& var) { return m_left->interpreter(var) + m_right->interpreter(var); } }; //减法解析器 class SubExpression : public SymbolExpression { public: SubExpression(Expression* left, Expression* right) : SymbolExpression(left, right) {}; ~SubExpression() {}; int interpreter(QMap<QString, int>& var) { return m_left->interpreter(var) - m_right->interpreter(var); } }; class Calculator { public: Calculator(QString expStr) : m_expression(nullptr) { init(expStr); }; ~Calculator() { deletetree(m_expression); m_expression = nullptr; } void deletetree(Expression* expression) { SymbolExpression* branch = dynamic_cast<SymbolExpression*>(expression); if (nullptr == branch) { delete expression; } else { deletetree(branch->getLeft()); deletetree(branch->getRight()); delete expression; } } int run(QMap<QString, int>& var) { if (nullptr == m_expression) { return 0; } return m_expression->interpreter(var); } private: void init(QString expStr) { QStack<Expression*> stkExp; Expression* left = nullptr; Expression* right = nullptr; for (quint32 i = 0; i < expStr.length(); i++) { if (‘+‘ == expStr.at(i)) { left = stkExp.top(); stkExp.pop(); right = new VarExpression(expStr.mid(++i, 1)); stkExp.push(new AddExpression(left, right)); } else if (‘-‘ == expStr.at(i)) { left = stkExp.top(); stkExp.pop(); right = new VarExpression(expStr.mid(++i, 1)); stkExp.push(new SubExpression(left, right)); } else { stkExp.push(new VarExpression(expStr.mid(i, 1))); } } if (!stkExp.empty()) { m_expression = stkExp.top(); stkExp.pop(); } } private: Expression* m_expression; }; #if 1 #define FREE_OBJ(obj) if (nullptr != (obj)){delete (obj); (obj) = nullptr;} int main() { QString expStr = "a+b-c"; QMap<QString, int> contextMap; var["a"] = 80; var["b"] = 66; var["c"] = 100; Calculator *cal = new Calculator(expStr); qDebug() << "result:" << expStr << " = " << cal.run(contextMap); FREE_OBJ(cal); return 0; } #endif // 1 #endif // !Interpreter.h
原文:https://www.cnblogs.com/yuemw/p/10339760.html