原理:
动态规划就是把一个大问题一步步降解成越来越小的子问题,直到子问题小到可以用确定的条件来解答。
但是动态规划的本质不是递归,递归是完全自顶而下的,每次求解都需要重新计算所有的子问题。
我觉得反映动态规划本质的解法是自底而上的解法,即按照顺序,从基元问题一步步扩大问题的规模,直到问题的规模覆盖了我要求解的问题。
每一个规模的问题的解叫做一个状态,每个不同规模的问题的解的关系叫做状态转移方程。具体的可以看凑硬币问题的具体分析。
1.凑硬币问题
问题: 有1元、3元、5元面值的硬币若干,要凑到11元需要最少几个硬币?
这是最简单的DP问题,记凑a元需要b个硬币为: n[a] = b。
1)首先,如果凑0元 需要0个硬币表示为 n[0] = 0
2)如果凑1元: 我们最近拿硬币的那次有三种可能 :拿了1元、3元、5元。
于是问题表示为:n[1] = 1+n[0] 或者 1+n[-2]或者 1+n[-4]。是这三种情况的最小值。但是没有凑-2或者凑-4元的情况,所以n[1] = 1+n[0]
3)凑2元:我们最近拿硬币的那次有三种可能 :拿了1元、3元、5元。
n[2] = min{ 1+n[1], 1+n[-1],1+n[-3] } = 1+n[1],而n[1]已经从上一步知道了
4)凑3元....
凑4元.....
.......
凑11元: 我们最近拿硬币的那次有三种可能 :拿了1元、3元、5元。
n[11] = min{ 1+n[10], 1+n[8], 1+n[6] } ,这里的n[10],n[8],n[6]在前几步就已经被算出来了,所以我们在这一步只要求个最小值就好了。
每一个新的状态都是由 “最近一个可能的动作”+“做该动作的上一个状态”确定而转移来的,这就是最基本的状态转移。这个问题的状态转移方程就可以看为:
n[m] = min{ 1+n[m-1], 1+n[m-3], 1+n[m-5] }
#最像伪代码的写法
def coins(M):
n = [0]
for N in range(1,M+1):
l = []
for i in [1,3,5]:
if N-i >= 0:
l.append(n[N-i]+1)
n.append(min(l))
return n
print(coins(11))
#out:[0, 1, 2, 1, 2, 1, 2, 3, 2, 3, 2, 3]
def coins(M): n = [0] for N in range(1,M+1): l = [] print(‘%%%%%%‘,N) for i in [1,3,5]: if N-i >= 0: l.append(n[N-i]+1) print(‘----‘,min(l)) n.append(min(l)) print(‘########‘,n) return n print(coins(11))
%%%%%% 1
---- 1
######## [0, 1]
%%%%%% 2
---- 2
######## [0, 1, 2]
%%%%%% 3
---- 1
######## [0, 1, 2, 1]
%%%%%% 4
---- 2
######## [0, 1, 2, 1, 2]
%%%%%% 5
---- 1
######## [0, 1, 2, 1, 2, 1]
%%%%%% 6
---- 2
######## [0, 1, 2, 1, 2, 1, 2]
%%%%%% 7
---- 3
######## [0, 1, 2, 1, 2, 1, 2, 3]
%%%%%% 8
---- 2
######## [0, 1, 2, 1, 2, 1, 2, 3, 2]
%%%%%% 9
---- 3
######## [0, 1, 2, 1, 2, 1, 2, 3, 2, 3]
%%%%%% 10
---- 2
######## [0, 1, 2, 1, 2, 1, 2, 3, 2, 3, 2]
%%%%%% 11
---- 3
######## [0, 1, 2, 1, 2, 1, 2, 3, 2, 3, 2, 3]
[0, 1, 2, 1, 2, 1, 2, 3, 2, 3, 2, 3]
当然从递归的角度,底顶而下,一次性的解决这个问题也是可以的。不过,递归的解法在每次需要用到子问题的结果时,即使刚刚算过这个子问题,它也会忘掉结果,重新把子问题递归到最底层求解,所以复杂度比较高。
def coins_rec(M):
if M == 0:
return 0
l = []
for i in [1,3,5]:
if M - i >= 0:
l.append( coins_rec(M-i)+1 )
return min(l)
print(coins_rec(11))
#out:3
回头看刚刚的动态规划写法,其实这里用到了一个memo,即代码里面的n[] 数组,来从小到大的储存每一个已经解决的子问题的解,后面再需要用到该问题的解时,不需要重新算,读出来就行了。下面我们比较一下两种方法所用的时间。还是差距很大的。
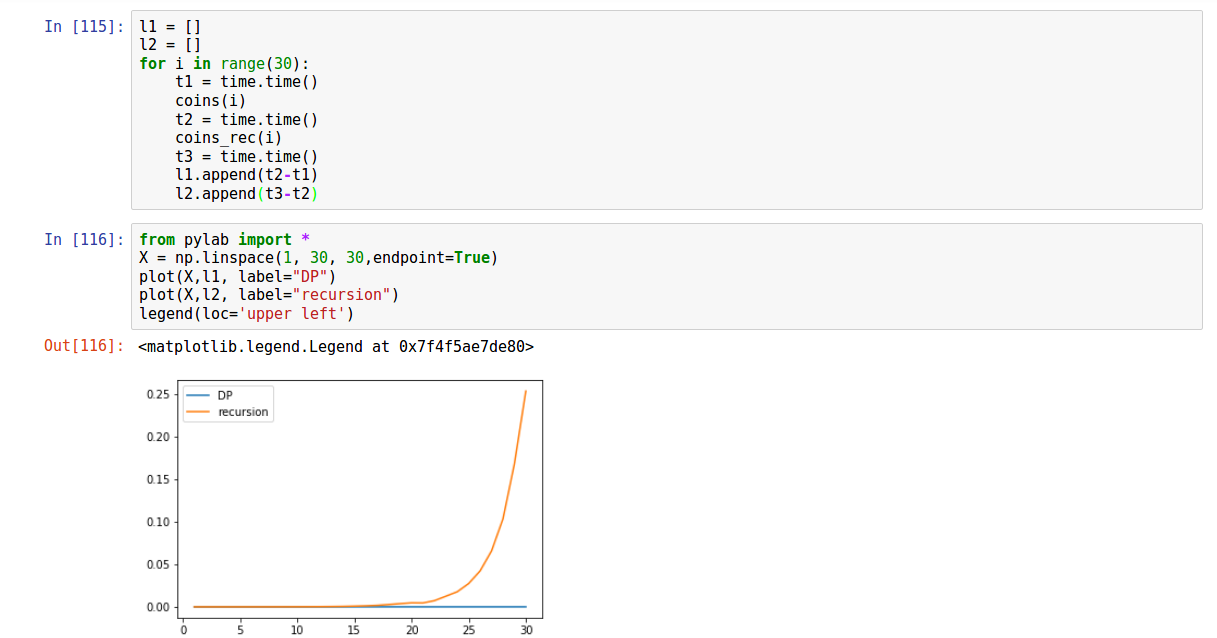
如果想要输出最小个数的同时输出组合的面值,就每次记录一下在 [1,3,5]这三个动作中,选取最小值时候使用的动作。
def cal_memo(M):
n = [0]
change = [0]
process = []
for N in range(1,M+1):
min_index = 100
min_number = 100
for i in [1,3,5]:
if N-i >= 0:
if n[N-i]+1 < min_number:
min_index = i
min_number = n[N-i]+1
n.append(min_number)
change.append(min_index)
index = M
while(index >0 ):
process.append(change[index])
index = index - change[index]
return n[M],process
print(cal_memo(11))
#out:(3, [1, 5, 5])
2.切刚条问题
问题:有一段长长的刚条可以切断成若干节来卖,长度为0-10的刚条单独卖的价格为:p = [0,1,5,8,9,10,17,17,20,24,30]。 问长度为n的刚条,最好的切割方法是什么?
可以看出,长度为2的刚条单独卖5元,切成2个长度为1的就只能卖2元了。而长度4的刚条9元,切成2个长度2的就是10元。所以贪心法是不对的。假设长度为n的刚条经过最优切割方案卖出的价格是 F[n]。可以把这个F[n]看成一个状态。其实我在做DP的时候,喜欢先找状态转移的条件,就是每一步可以有的动作,这里动作就是最近一次切下来长度为m的一部分,得到的新状态可以用旧状态表示为: F[n] = p[m]+F[n-m],当然我们的m需要遍历[1,2,....10] (n-m >= 0)。为什么不要0?因为和之前的凑硬币一样的,我们从F[0],F[1]一步步扩展的,多切一小段长度1出来肯定多卖一点钱。
最像伪代码的代码,直接把扩展的过程print出来了。要输出长度的组合和凑硬币一样,记录一下每一步切割的长度就好
def Cut(n):
p = [0,1,5,8,9,10,17,17,20,24,30]
F = [0]
for i in range(1,n+1):
l = []
for m in range(1,11):
if i-m >= 0:
l.append(p[m] + F[i-m])
F.append(max(l))
print(i,F)
return F
print(Cut(20))

3.LCS问题
最长公共子序列问题:有X Y两个序列,求最长的公共子序列的长度。举例:
X: ABCBDAB
Y: BDCABA
最长的子序列为长度为4,有好几条,比如:BDAB BCAB。
分析:基元的问题是x = X[:0], y = Y[:0]都是空序列,LCS(x,y) = 0。然后可以采取的动作是把X向后扩展一位或者把Y向后扩展一位。我们这里就X:求LCS(X[:1],Y[:0] ) = 0发现扩X没用的,Y[:0]是空的...所以LCS(X[:2],Y[:0] ) = 0....LCS[X,Y[:0]] = 0.我们这样一步步刷过去,相当于在一个 len(Y)+1 * len(X)+1的表格里面一行一行的从左到右算出每个A B部分对应的LCS。
在中间我们发现要填写LCS( X[:i], Y[:j])时,自然想到
如果X[i] = Y[j]那么LCS( X[:i], Y[:j]) = 1+LCS( X[:i-1], Y[:j-1]) 。而由于我们是一行行刷过来的,LCS( X[:i-1], Y[:j-1])求过了。
如果X[i] != Y[j]那么LCS( X[:i], Y[:j]) = max{ LCS( X[:i], Y[:j-1]), LCS( X[:i-1], Y[:j]) }。这俩也都求出来了,所以这也就是一个填表的过程
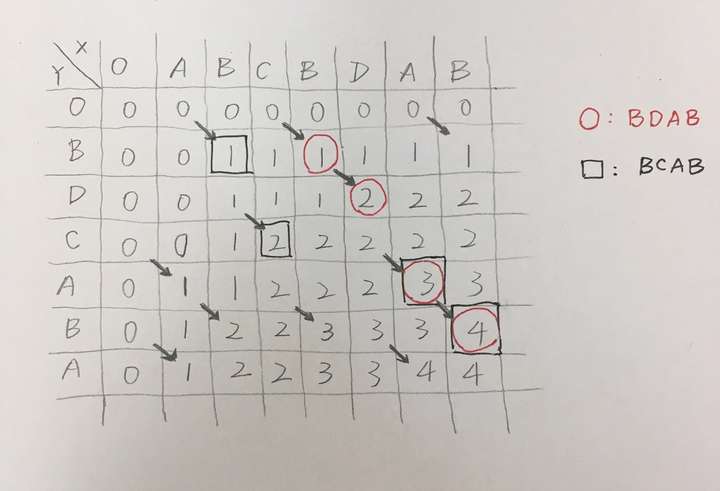
一行一行从左到有填过来的。可以回头找到好几组不同的最长子序列。箭头表示Y[i] = X[j]的状态转移。如果要print具体的子序列,就需要记录一下i,j
最像伪代码的代码:
import numpy as np
def LCS(X,Y):
table = np.zeros([len(Y)+1,len(X)+1])
for i in range(1, len(Y)+1):
for j in range(1,len(X)+1):
if Y[i-1] == X[j-1]: # 这里-1是因为表格补了一行一列空元素,所以序号错开了
table[i,j] = table[i-1,j-1]+1
else:
table[i,j] = max( table[i,j-1], table[i-1,j])
return table
LCS("ABCBDAB","BDCABA")

变一点点:如果要求连续的公共最长子序列。
如果X[i] = Y[j]那么LCS( X[:i], Y[:j]) = LCS( X[:i-1], Y[:j-1])
如果X[i] != Y[j]那么LCS( X[:i], Y[:j]) = 0,就相当于在这里重新开始了。
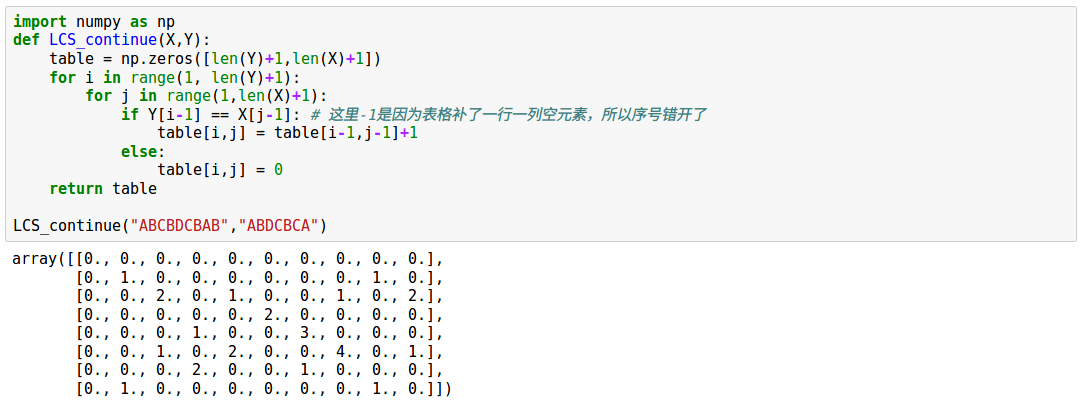
原文:https://www.cnblogs.com/the-wolf-sky/p/10353170.html