前面介绍的二叉搜索树在最坏情况下的性能还是很糟糕,而且我们不能控制操作的顺序,有时根本就不是随机的,我们希望找到有更好性能保证的算法。
于是先来了解下 2-3 查找树,它可以保证树的平衡性,维护树高在 lgN 级别。这里的 2,3 指的是孩子的数目,图例:
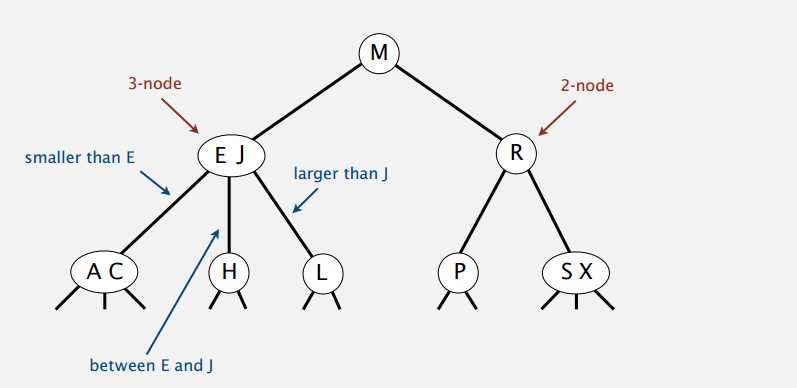
有两个孩子的节点和二叉搜索树一样,节点里有一个键,且大于左子树的键并小于右子树的键。三个孩子的节点里则有两个键,中间孩子的键的大小介于这两个键之间,左右子树一样。
查找和二叉查找树一样,虽然现在有的点有两个键,但是也没有什么关系。
查找图例:
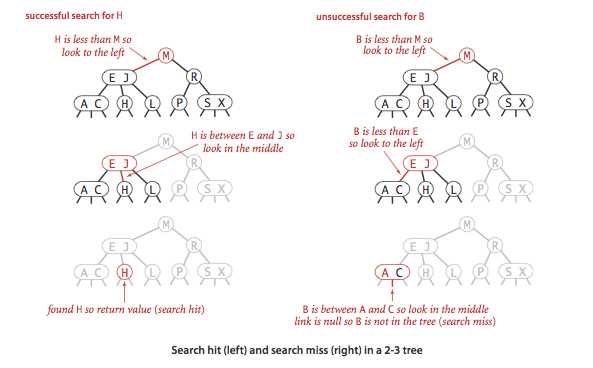
插入操作比较关键,解释了为什么可以保证树的平衡性,下面是各种情况的示意:
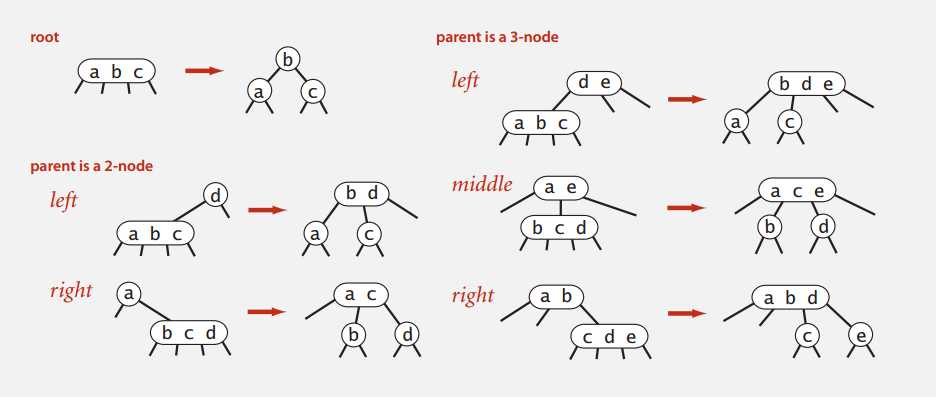
插入 2-node 时,直接插入把这个节点变成 3-node 即可,上面也没有列出来。插入 3-node 时比较复杂,要先暂时变成 4-node,然后再把三个键中间的键向父母节点转移,问题就又转移到了父母节点上。不难发现,只有在插入路径上全部都是 3-node 时,插入才会让树的高度加一(一路到根节点变成上图情况一)。
而且,上面的操作找到位置后只是改变链接的局部变换,没有数据转移什么的,时间很快,效率挺高。最坏情况下都是 2-node,树高为 lgN,最好情况下都是 3-node,树高为 \(log_{3}N \approx .631 lgN\),反正树高是对数级别,也就保证了查找和插入对数级别的性能。
但是吧,谈到实现,直接实现太复杂,有好多不同类型的节点,还要进行类型转换,而且需要处理的情况也有很多。实现这些不仅需要大量的代码,而且它们产生的额外开销可能会使算法比标准的二叉查找树更慢。我们希望维护树的平衡,同时也希望保障所需的代码能够越少越好。于是乎,红黑树出现啦!
红黑树本质上还是二叉树,关键是在标准二叉查找树的基础上添加了一些信息来表示 3-node:
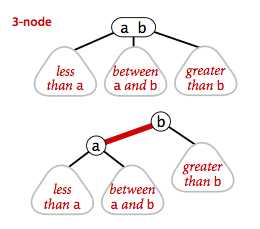
3-node 里的两个键用左斜的红链接连接,较大的键为根,任意的 2-3 树都有唯一的红黑树与之对应:
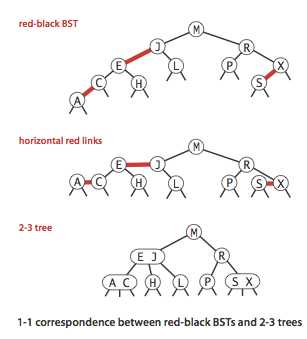
在这样的表示下,显然不存在有两条红链接的节点,而且任意从根节点到空链接的路径上的黑链接数都是一样的(perfect black balance),还有注意红链接是左连接,在构建的时候要维护这些性质。
每个节点都只有一条来自父母的链接,我们可以借此表示链接的颜色:
代码:
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node {
Key key;
Value val;
Node left, right;
boolean color; // color of parent link
}
private boolean isRed(Node x) {
if (x == null) return false; // null link is black
return x.color == RED;
}图例:
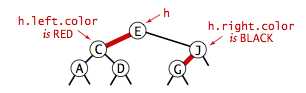
红黑树下的查找操作不需要考虑链接的颜色,和二叉查找树一模一样,因为更好的平衡还会快些。
代码:
public Value get(Key key) {
Node x = root;
while (x != null) {
int cmp = key.compareTo(x.key);
if (cmp < 0) x = x.left;
else if (cmp > 0) x = x.right;
else return x.val;
}
return null;
}其它一些只要比较而不会破坏树结构的顺序相关操作也是,直接用原来二叉查找树的代码就好,主要还是看插入操作。
回想 2-3 树的插入操作,实际上都是直接来,性质被破坏了再调整。像 2-node 就直接变成 3-node,而 3-node 会暂时变成 4-node,然后再去调整。红黑树也是这样,新加入一个节点时,都把新链接认为是红色的,不符合性质再调整,像链接不是左斜或是一个节点有两个红链接。
所以,来了解下为了维护性质的调整操作。
左旋,顾名思义就是把红链接从右斜转到左斜。

右旋和左旋相反,这是一个中间状态,有时候需要先右旋再处理才行,下面会见到。

颜色转换,甚至不需要改变任何链接,只要改变颜色就好。
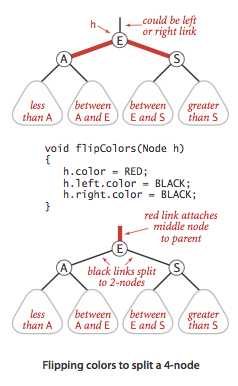
虽然红黑树的插入情况看起来好像很多,但是其实可以用下图来概括(最左边的就要先右旋):

处理也只要统一用下面的代码就好:
private Node put(Node h, Key key, Value val) {
// insert at bottom(and color it red)
if (h == null) return new Node(Key, val, RED);
int cmp = key.compareTo(h.key);
if (cmp < 0) h.left = put(h.left, key, val);
else if (cmp > 0) h.right = put(h.right, key, val);
else h.val = val;
if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h); // lean left
if (isRed(h.left) && isRed(h.left.left)) h = rorateRight(h); // balance 4-node
if (isRed(h.left) && isRed(h.right)) flipColors(h);
return h;
}最后,再来张构造的示例图感受下:
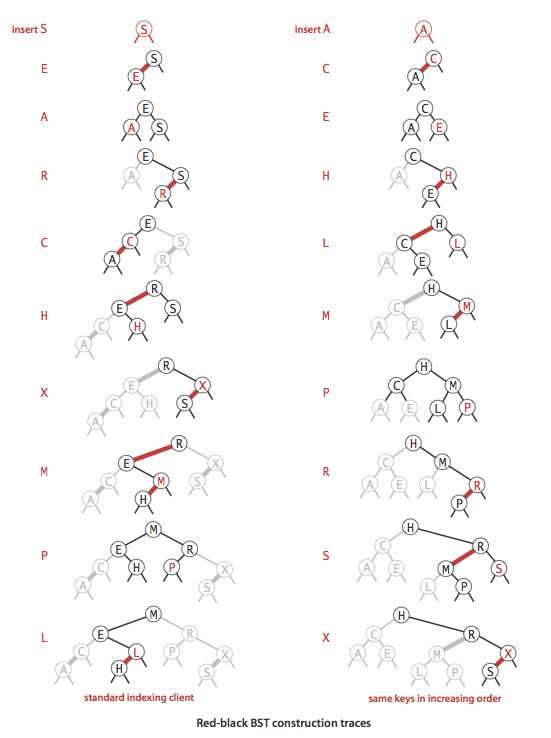
左边一开始的 S,E,A 会形成再上一张图最左边的情况,先对 S 右旋成最右边情况再转换颜色;接下来的 R 很顺利,而 C 会插到 A 的右边形成右斜红链接,需要左旋;H 的插入到 R 的左孩子,这时 S 的左孩子和左孙子的链接都是红色需要右旋,然后 R 两个孩子链接都是红色,转换颜色,之后 E 的右链接变成红色需要左旋...
性能方面,可以保证操作复杂度都是对数级别,一棵大小为 N 的红黑树的高度不会超过 2lgN(证明不管啦)。然后还有其它操作,像删除(更复杂),请参见:RedBlackBST.java。
B 树是一个非常典型的红黑树的实际应用,是平衡树的泛化,每个节点里可以有很多键。因为通常来说,我们需要存储的数据非常大,找到存储数据所在页的时间要比从页里读取数据慢得多,所以我们希望能尽快定位特定的页。B 树每个节点可以有很多很多键,多到可以放一整页的那种:
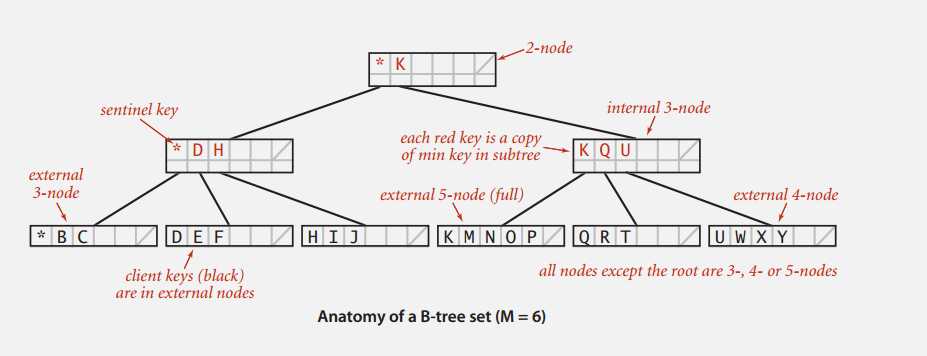
根节点至少有两个键,内部结点维护键的副本来指导搜索,实际上键有序存储在外部节点上,节点键的数量在 M/2 到 M-1 之间。
查找老样子,来个例子看下:
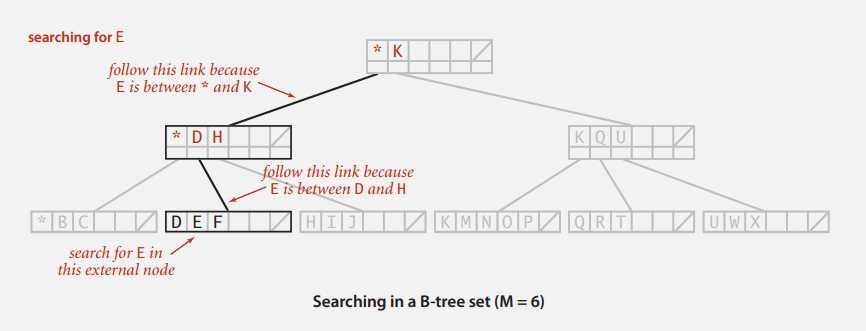
插入的时候要注意维护树的平衡性,键数目达到 M 的节点需要分裂并向上调整,例图:
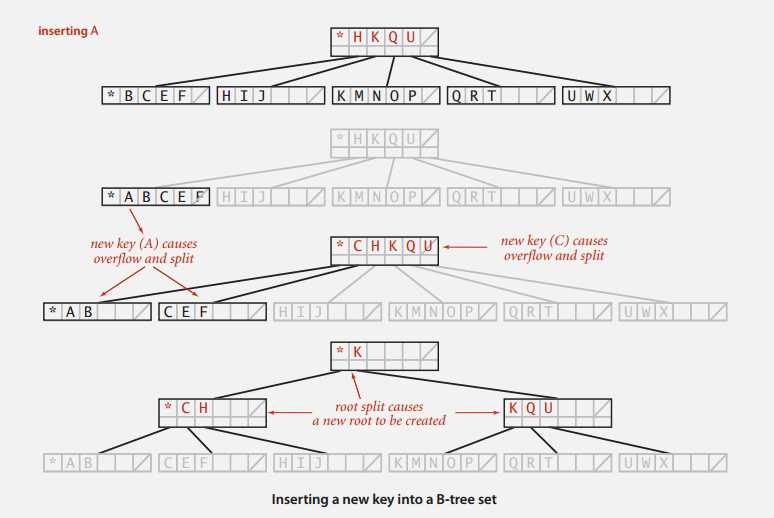
因为完美的平衡性,找到特定页的复杂度在 \(log_{M-1}N\) 和 \(log_{M/2}N\) 之间,实际中一般最多只要四次(M =1024; N = 62 billion; \(log_{M/2} \leqslant 4\))。
再贴张 B 树成长的示意图(我都截了):
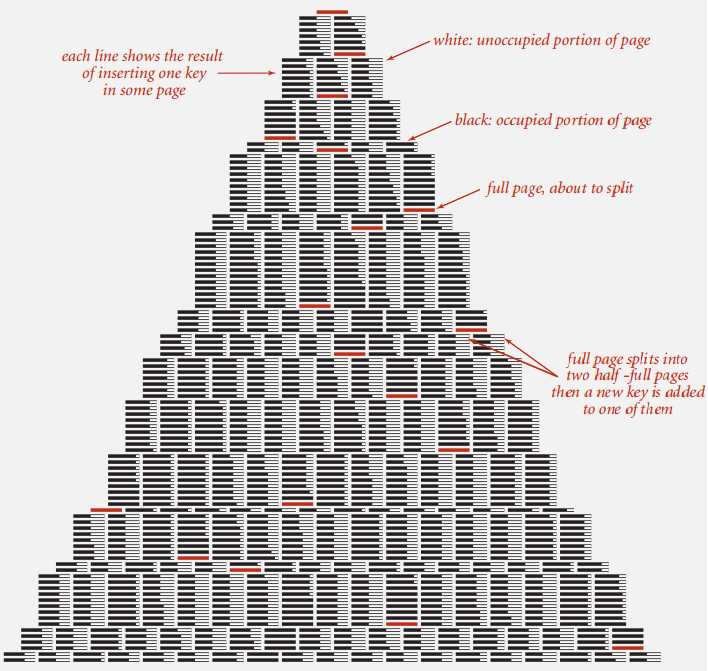
每一行表示新插入一个键,红色的表示页饱和需要分裂调整。
红黑树被广泛地应用于系统符号表中,Java util 里的 TreeMap 和 TreeSet,C++ STL 里的 map,multimap,multiset 等。
原文:https://www.cnblogs.com/mingyueanyao/p/10322643.html