Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 25649 Accepted Submission(s): 11635
这道题我一开始用的大数求阶乘的方法做的,结果超时,O(N2)的算法伤不起。
先挂一下超时的代码

1 #include<cstdio> 2 #include<cstring> 3 #include<stdlib.h> 4 #include<algorithm> 5 using namespace std; 6 int main() 7 { 8 int kase,num[3000],i,j; 9 scanf("%d",&kase); 10 while(kase--) 11 { 12 int n; 13 scanf("%d",&n); 14 memset(num,0,sizeof(num)); 15 num[0]=1; 16 for(int i=2;i<=n;i++) 17 { 18 int c=0; 19 for(int j=0;j<3000;j++) 20 { 21 num[j]=num[j]*i+c; 22 c=num[j]/10; 23 num[j]=num[j]%10; 24 } 25 } 26 for(i=2999;i>=0;i--) 27 if(num[i]) 28 break; 29 printf("%d\n",i+1); 30 } 31 return 0; 32 }
后来一想,就算不超时,10^7的阶乘也存不下,所以一时之间没有思路。
后来上网看大神怎么做的,才AC了。
如果要计算一个数num的位数,那么可以用到 (int)lg((double)num)+1
这里lg(1*2*3......n)=lg1+lg2+lg3+......lg n
这里的话可以将1~10^7的数的位数全部存起来,是一种打表的做法。

1 #include<cstdio> 2 #include<cmath> 3 #include<cstring> 4 #include<stdlib.h> 5 using namespace std; 6 int a[10000005]; 7 int main() 8 { 9 a[1]=1; 10 double sum=0; 11 for(int i=2;i<=10000000;i++) 12 { 13 sum+=log10((double)i); 14 a[i]=sum+1; 15 } 16 int kase,n; 17 scanf("%d",&kase); 18 while(kase--) 19 { 20 scanf("%d",&n); 21 printf("%d\n",a[n]); 22 } 23 return 0; 24 }
当然还有一种做法就是用到了斯特林数
公式为:
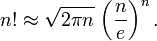
求出阶乘然后同样的方法取位数,求出lg(n!)再向上取整

1 #include<cstdio> 2 #include<cmath> 3 #include<cstring> 4 #include<stdlib.h> 5 const double PI=3.141592654; 6 const double e=2.718281828; 7 using namespace std; 8 int main() 9 { 10 int kase,n; 11 double sum; 12 scanf("%d",&kase); 13 while(kase--) 14 { 15 scanf("%d",&n); 16 sum=log10(2*PI*n)/2+n*log10(n/e); 17 printf("%d\n",(int)sum+1); 18 } 19 return 0; 20 }
HDU 1018 Big Number (简单数学),布布扣,bubuko.com
原文:http://www.cnblogs.com/clliff/p/3891580.html