/* 可持久化的迹象,我们俯身欣赏! ——《膜你抄》 */
我们在生活中可能会遇到这样的问题,要是某一变化是基于某一个历史版本而来的变化。
这样处理的过程就比较困难。(然而对于暴力这个一点都不困难)
有什么是暴力算法解决不了的呢?
又有什么暴力算法是优化不了的呢?
我们分析暴力算法的复杂度(裸暴力我们就不说了)
考虑有点技术含量的暴力:我开M个数据结构维护每一时刻的版本然后在那一时刻的版本上做操作。
Hmm...复杂度是对了,但是空间呢?大概联赛给你开放整一个内存吧。(可能还不够。。。)
我们分析这样的劣势:就是把以前一样的东西重复记录的M次。
要是我们只改变有修改部分的结构就好了!!!
于是就有了可持久化数据结构:我们只记录原来数据结构中发生改变的副本,其他的留在原数据结构中。
这个首先得搞懂思想(请确保读懂上面相关知识)
在可持久化Trie树中插入一个元素的步骤一般如下:
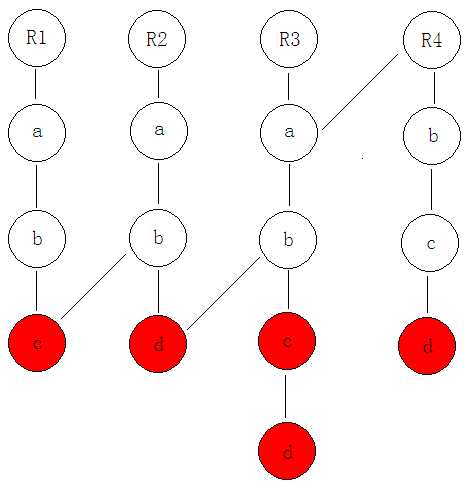
这里是对于四个字符串依次插入可持久化Trie树的图,结合上述思想理解一下:
这四个字符串依次是:“abc","abd","abcd","bcd”.
这里是一个例题:P4735 最大异或和
Solution:显然需要考虑前缀xor和,记为s[i]
对于询问操作 l,r , x 就是询问一个位子p∈[l-1,r-1]使s[p] xor (x xor s[n])
如果只考虑右端点限制,那么就是直接从root[r-1] 访问进去贪心选取就行,
我们再次考虑左端点的限制,那么我们记lastest[x]表示指针所指元素位子为x时,最后面元素插入时经过这个点的最大的序号。
(如果没有元素经过这个点置为最小值-1:我们坚决不访问他)
然后询问时候考虑左端点限制是在处理下一个点去哪的位置是last值必须大于等于l-1才被认为有效点,
然后剩下的贪心(走和当前位相反或者走有元素那边)就行。
Hint:本题卡常#3和#6点建议打上O2优化、快读、还有别打那么多头文件...

# pragma G++ optimize(2) # include <cstdio> using namespace std; const int N=600010; int n,m,tot; int trie[N*24][2],lastest[N*24],root[N],s[N]; inline int max(int x,int y){return (x>y)?x:y;} inline int read() { static char c= getchar(); int a= 0; while(c < ‘0‘ || c > ‘9‘) c= getchar(); while(c >= ‘0‘ && c <= ‘9‘) a= a * 10 + c - ‘0‘, c= getchar(); return a; } void insert(int i,int dep,int lstrt,int nowrt) { if (dep<0) { lastest[nowrt]=i; return;} int c=(s[i]>>dep) & 1; if (lstrt!=0) trie[nowrt][c^1]=trie[lstrt][c^1]; trie[nowrt][c]=++tot; insert(i,dep-1,trie[lstrt][c],trie[nowrt][c]); lastest[nowrt]=max(lastest[trie[nowrt][0]],lastest[trie[nowrt][1]]); } int ask(int nowrt,int val,int dep,int mark) { if (dep<0) return s[lastest[nowrt]]^val; int c=(val>>dep) & 1; if (lastest[trie[nowrt][c^1]]>=mark) return ask(trie[nowrt][c^1],val,dep-1,mark); else return ask(trie[nowrt][c],val,dep-1,mark); } inline void write(int x) { if (x>9) write(x/10); putchar(‘0‘+x%10); } int main() { n=read();m=read(); int t; lastest[0]=-1; root[0]=++tot; insert(0,23,0,root[0]); for (int i=1;i<=n;i++) { t=read(); s[i]=s[i-1]^t; root[i]=++tot; insert(i,23,root[i-1],root[i]); } char op[3]; for (int i=1;i<=m;i++) { scanf("%s",op); if (op[0]==‘A‘) { int x=read(); root[++n]=++tot; s[n]=s[n-1]^x; insert(n,23,root[n-1],root[n]); } else { int l=read(),r=read(),x=read(); write(ask(root[r-1],x^s[n],23,l-1)); putchar(‘\n‘); } } return 0; }
原文:https://www.cnblogs.com/ljc20020730/p/10353707.html