支持向量机（Support Vector Machine, SVM）是一种二分类模型。给定训练集D = {(x₁,y₁), (x₂,y₂), ..., (x_m,y_m)}，分类学习的最基本的想法即是找到一个超平面S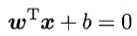：，从而将训练集D的样本空间中不同类别的样本区分开。

SVM的模型，由简至繁地，包括：线性可分支持向量机（linear SVM in linearly separable case）、线性支持向量机（linear SVM）以及非线性支持向量机（non-linear SVM）。

当训练数据线性可分时，SVM试图寻找硬间隔最大化（hard margin maximization）的划分超平面，因为这样的超平面产生的分类结果是最鲁棒的，由此学习的线性分类器称为线性可分支持向量机；而当训练数据近似线性可分时，通过软间隔最大化（soft margin maximization），也可学习得到分类器，称为线性支持向量机；当数据线性不可分时，则可以使用核技巧（kernel trick）以及软间隔最大化，习得非线性支持向量机。“间隔|、”核技巧“等相关概念均将在下文中予以阐述。

一、线性可分支持向量机

 1.1 间隔与支持向量

如前文所述，划分超平面可以用线性方程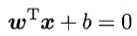来描述，其中ω为法向量，b为位移。于是，划分超平面可以由ω和b确定，记为(ω, b)。利用高中解析几何的相关知识容易推算出，样本空间中任意点到超平面(ω, b)的距离即为

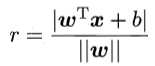
由于若超平面(ω‘, b‘)可以对样本正确分类，则对于(x_i,y_i)，若y_i=+1，则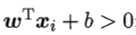；若y_i=-1，则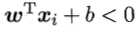。令

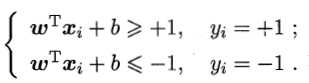
则总存在缩放变换?ω→ω‘,?b→b‘使得上式成立。由此，定义”支持向量“（support vector）为满足上式且距离超平面最近的点。两个异类支持向量到超平面的距离之和被称为”间隔“（margin），为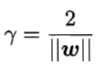。顺便一提，所谓样本都必须划分正确的情形称为”硬间隔“（hard margin），而”软间隔“（soft margin）则允许某些样本不满足。

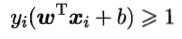SVM的任务是找到”最大间隔“（maximum margin）的划分超平面。于是，SVM的基本型可以表达为

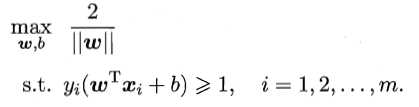
进而可以写为

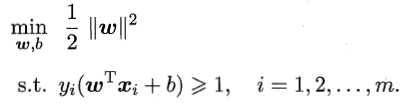
值得注意的是，间隔貌似只与ω有关，但事实上，b通过约束隐式地影响着ω的取值，进而对间隔产生影响。

1.2 对偶问题与SMO算法

为求解得到最大间隔划分超平面的模型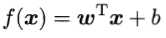，一种高效的办法是利用lagrange乘子法得到SVM基本型的”对偶问题“（dual problem），再利用SMO算法求解。

首先，在基本型中，对每条约束添加lagrange乘子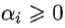，得到lagrange函数为

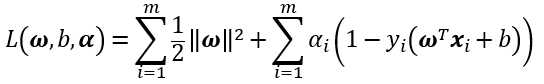
为取到函数的最值，令L(ω,b,α)对ω和b分别求偏导为零，得到

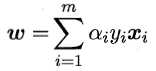
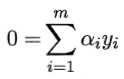
代入L(ω,b,α)，消去ω和b，即得到SVM基本型的对偶问题

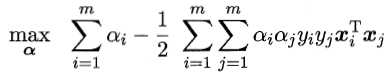
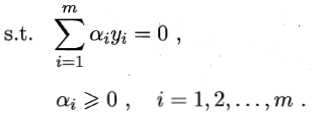
且上述过程需要满足KKT条件，即要求

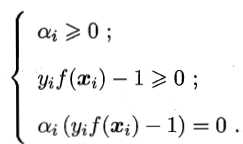
直接用二次规划算法来求解对偶问题，开销较大。比较高效的是SMO算法（Sequential Minimal Optimization）。

SMO首先初始化参数，然后不断执行下述步骤直至收敛：

• 选取一对需要更新的α_i和α_j；
  
• 固定α_i和α_j以外的参数，求解上式获得更新后的α_i和α_j。

最后，由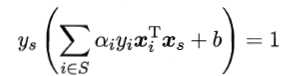，可以确定偏移项b为

1.3 核函数

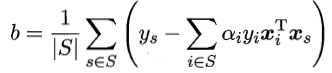
如果原始样本空间中不存在可以正确划分样本的超平面，则可以将样本从原始空间映射到更高维的特征空间，使得样本在此特征空间内线性可分。事实上，若原始空间是有限维的，则一定存在一个更高维的空间使样本线性可分。

令Φ(x)表示将x映射后的特征向量，则在特征空间中，划分超平面对应的模型可表示为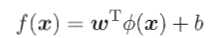。于是得到基本型

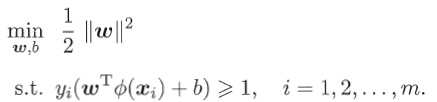
及其对偶问题

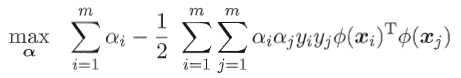
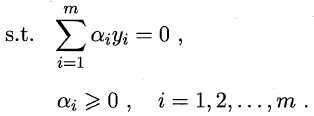
直接计算Φ(x_i)^TΦ(x_j)通常比较困难，为此，引入”核函数“（kernel function）k(?,?)。设k(x_i, x_j) = <Φ(x_i), Φ(x_j)> = Φ(x_i)^TΦ(x_j)，则对偶问题可以重写为

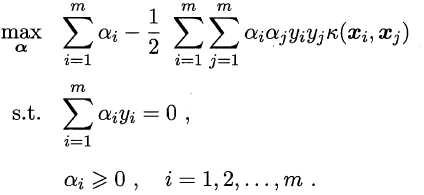
求解后即得到

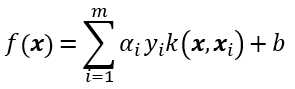
此展式亦称为”支持向量展式“（support vector expansion）。

那么，合适的核函数是否一定存在？什么样的核函数能作为核函数呢？对此，有如下定理：

定理 令为输入空间，k(?,?)为定义在上的对称函数，则k是核函数当且仅当对于任意数据D = {x₁,x₂,...,x_m}，”核矩阵“（kernel matrix）K总是半正定的：

书中给出了几种常见的核函数，见于下表

此外，核函数还可以通过函数组合得到：

• 若k₁和k₂是核函数，则k₁(x,z)k₂(x,z)也是核函数；
• 若k₁是核函数，则对于任意函数g(x)，k(x,z) = g(x)k₁(x,z)g(z)也是核函数。

支持向量机（SVM）

原文：https://www.cnblogs.com/Jeffrey-Y/p/10366622.html