学过数据结构和会做题完全是两个概念orz
各种各样的题目都应该见识一下
最大连续长度问题
典型题目:HDU 3911 (Black And White)
题目大意:有一个长度为n(1≤n≤105)的01序列ai,现在有m个操作:将区间[li,ri]反转(01互换),或询问区间[li,ri]中1最多连续出现多少次
区间的反转很显然可以用懒标记解决,细节就不再赘述了(比如打完标记向上更新啥的一开始我就忘了orz)
难办的是区间内的最大连续长度,原因在于,两段小区间如何合并成一个大区间并不容易想到
先考虑最大连续长度可能的来源
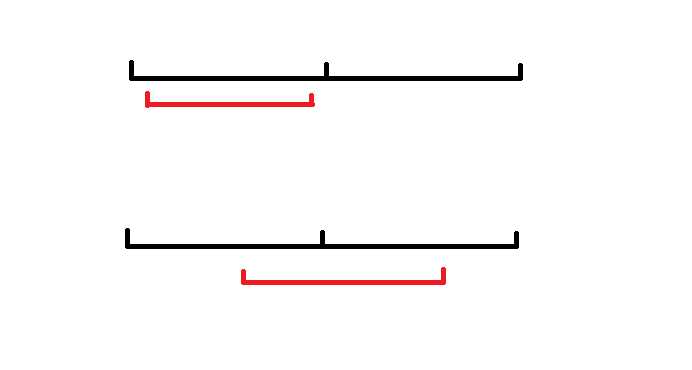
我们可以多记录一东西:除了当前区间内的最大连续长度,再记录当前区间内从最左端、最右端开始的最大连续长度
这样,如果我们想把两个小区间合并,得到的连续长度相当于是(左半区间从右端开始的最大长度+右半区间从左端开始的最大长度)
这两个新加的记录值也是容易合并的:求最左端开始的最大连续长度,如果左半区间全是相同数字,那么可以与右半区间的最左端合并,否则就是左半区间的最大连续长度;求最右端开始的亦是如此
所以本题的启示是,加入一些新的记录值来帮助计算

#include <cstdio> #include <cmath> #include <cstring> #include <cstdlib> using namespace std; inline int max(int a,int b) { return (a>b?a:b); } inline int min(int a,int b) { return (a<b?a:b); } inline void swap(int &a,int &b) { int tmp=a; a=b,b=tmp; } const int MAX=100005; int n,m; int c[MAX<<1]; int sz; int left[MAX<<2][2],right[MAX<<2][2],mid[MAX<<2][2]; int tag[MAX<<2]; inline void Calc(int k,int a,int b) { int len=(b-a+1)>>1; for(int i=0;i<2;i++) { left[k][i]=left[k<<1][i]+(left[k<<1][i]==len?left[(k<<1)+1][i]:0); right[k][i]=right[(k<<1)+1][i]+(right[(k<<1)+1][i]==len?right[k<<1][i]:0); mid[k][i]=max(mid[k<<1][i],mid[(k<<1)+1][i]);//#1 mid[k][i]=max(mid[k][i],right[k<<1][i]+left[(k<<1)+1][i]); } } inline void Build(int k,int a,int b) { if(a==b) { left[k][c[a]]=right[k][c[a]]=mid[k][c[a]]=1; return; } Build(k<<1,a,(a+b)>>1); Build((k<<1)+1,((a+b)>>1)+1,b); Calc(k,a,b); } inline void Update(int k,int a,int b) { if(!tag[k]) return; swap(left[k][0],left[k][1]); swap(right[k][0],right[k][1]); swap(mid[k][0],mid[k][1]); tag[k]=0; if(a!=b) { tag[k<<1]^=1; tag[(k<<1)+1]^=1; } } inline void Modify(int k,int l,int r,int a,int b) { Update(k,a,b); if(a>r || b<l) return; if(a>=l && b<=r) { tag[k]^=1; Update(k,a,b); return; } Modify(k<<1,l,r,a,(a+b)>>1); Modify((k<<1)+1,l,r,((a+b)>>1)+1,b); Calc(k,a,b); } inline int Query(int k,int l,int r,int a,int b) { Update(k,a,b); if(a>r || b<l) return 0; if(a>=l && b<=r) return mid[k][1]; int half=(a+b)>>1; if(r<=half) return Query(k<<1,l,r,a,half); if(l>half) return Query((k<<1)+1,l,r,half+1,b); int midv=max(Query(k<<1,l,r,a,half),Query((k<<1)+1,l,r,half+1,b)); midv=max(midv,min(right[k<<1][1],half-l+1)+min(left[(k<<1)+1][1],r-half)); return midv; } int main() { // freopen("input.txt","r",stdin); while(~scanf("%d",&n)) { memset(left,0,sizeof(left)); memset(right,0,sizeof(right)); memset(mid,0,sizeof(mid)); memset(tag,0,sizeof(tag)); memset(c,0,sizeof(c)); for(int i=1;i<=n;i++) scanf("%d",&c[i]); sz=1; while(sz<n) sz<<=1; Build(1,1,sz); scanf("%d",&m); while(m--) { int op,x,y; scanf("%d%d%d",&op,&x,&y); if(op==1) Modify(1,x,y,1,sz); else printf("%d\n",Query(1,x,y,1,sz)); } } return 0; }
(待续,慢慢补题)
原文:https://www.cnblogs.com/LiuRunky/p/Segment_Tree.html