给定AA、BB、CC三根足够长的细柱,在AA柱上放有2n2n个中间有孔的圆盘,共有nn个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为n=3n=3的情形)。
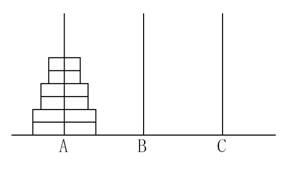
现要将这些圆盘移到CC柱上,在移动过程中可放在BB柱上暂存。要求:
(1)每次只能移动一个圆盘;
(2)AA、BB、CC三根细柱上的圆盘都要保持上小下大的顺序;
任务:设A_nAn?为2n2n个圆盘完成上述任务所需的最少移动次数,对于输入的nn,输出A_nAn?。
输入格式:
一个正整数nn,表示在AA柱上放有2n2n个圆盘。
输出格式:
一个正整数, 为完成上述任务所需的最少移动次数A_nAn?。
【限制】
对于50%的数据,1≤n≤25
对于100%的数据,1≤n≤200
通过模拟1-5,你可以发现一个关系式a[i]=(2i-1)*2。
只需要将a数组求出即可(不需用数组,直接求a[i])。
数据n很大,去要用高精乘和高精加。
for(int i=1;i<=n+1;i++){ for(int j=1;j<=a[0];j++){ a[j]=a[j]*2+jw; jw=a[j]/10; a[j]=a[j]%10; } while(jw!=0){ a[0]++; a[a[0]]=jw%10; jw=jw/10; } }
j=0; while(true){ j++; a[j]=a[j]-2-qw; jw=0; while(a[j]<0){ qw++; a[j]=a[j]+10; } if((j=a[0])||(qw=0)) break; } if(qw!=0){ a[0]++; a[a[0]]=qw; }
#include<iostream> #include<cstring> using namespace std; int n; int a[1000]; int jw,qw,j; int main(){ cin>>n; a[0]=1; a[1]=1; for(int i=1;i<=n+1;i++){ for(int j=1;j<=a[0];j++){ a[j]=a[j]*2+jw; jw=a[j]/10; a[j]=a[j]%10; } while(jw!=0){ a[0]++; a[a[0]]=jw%10; jw=jw/10; } } j=0; while(true){ j++; a[j]=a[j]-2-qw; jw=0; while(a[j]<0){ qw++; a[j]=a[j]+10; } if((j=a[0])||(qw=0)) break; } if(qw!=0){ a[0]++; a[a[0]]=qw; } for(int i=a[0];i>=1;i--) cout<<a[i]; return 0; }
原文:https://www.cnblogs.com/zhouxuanbodl/p/10388643.html