P1880 [NOI1995]石子合并

先来介绍一下四边形不等式吧

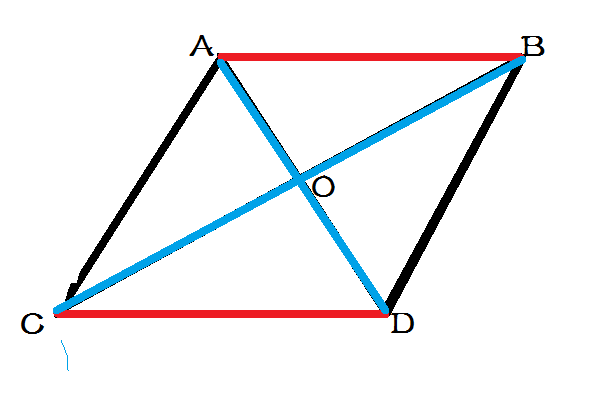
如图，这是一个四边形，看着是一个平行四边形，但他不是（我说不是就不是）

易知，AB+CD <= AD+CB

很容易证明，记中心交点为 O ，在 Rt\(_\bigtriangleup\)AOB 和 Rt\(_\bigtriangleup\)COD 中

任意两边之和大于第三边

所以两者相加，则有了四边形不等式

• 定理一：如果一个函数w(i,j)同时满足区间包含单调性和四边形不等式性质，那么函数:

  m(i,j) = min{} + w(i,j) 也满足四边形不等式性质。

• 定理二：假如m(i,j)满足四边形不等式，那么s(i,j)单调，即s(i,j)≤s(i,j+1)≤s(i+1,j+1)。

• s(i,j) 函数代表党m(i,j) 函数取最优值时的分割线处

来看这道题

n^3的应该都会吧

#include <bits/stdc++.h>
#define ll long long 
#define E 207
using namespace std ; 
ll n , a[E] , f[E][E] , p[E][E] , minn = 0x7ffffffffffLL , maxn , sum[E] ; 
ll read() { ll aa ; cin >> aa ; return aa ; }
int main() {
    n = read() ; 
    for(int i = 1 ; i <= n ; i ++) a[i] = a[i+n] = read() ; 
    for(int i = 1 ; i <= n*2 ; i ++) sum[i] = sum[i-1] + a[i] ; 
    for(int d = 2 ; d <= n ; d ++) {
        for(int i = 1 ; i+d-1 <= n*2 ; i ++) {
            ll j = i + d - 1 ; 
            f[i][j] = 0x7ffffffffffLL ; 
            for(int l = i ; l < j ; l ++) {
                f[i][j] = min(f[i][l]+f[l+1][j] + sum[j]-sum[i-1] , f[i][j]) ; 
                p[i][j] = max(p[i][l]+p[l+1][j] + sum[j]-sum[i-1] , p[i][j]) ;
            }
        if(d == n) minn = min(f[i][j] , minn) , maxn = max(p[i][j] , maxn) ; 
        }
    }
    cout << minn << endl << maxn << endl ; 
    return 0 ; 
}

引用并推荐

看我优化 （玄学）

#include <bits/stdc++.h>
#define ll long long 
#define E 207
using namespace std ; 
ll n , a[E] , f[E][E] , p[E][E] , s[E][E] , minn = 0x7ffffffffffLL , maxn , sum[E] ; 
ll read() { ll aa ; cin >> aa ; return aa ; }
int main() {
    n = read() ; 
    for(int i = 1 ; i <= n ; i ++) a[i] = a[i+n] = read() ; 
    for(int i = 1 ; i <= n*2 ; i ++) sum[i] = sum[i-1] + a[i] , s[i][i] = i ; 
    for(int d = 2 ; d <= n ; d ++) {
        for(int i = 1 ; i+d-1 <= n*2 ; i ++) {
            ll j = i + d - 1 ; 
            p[i][j] = max(p[i][j-1]+0 , p[i+1][j]+0) + sum[j]-sum[i-1] ; 
            f[i][j] = 0x7ffffffffffLL ; 
            for(int l = s[i][j-1] ; l <= s[i+1][j] ; l ++) {
                if(f[i][l]+f[l+1][j] + sum[j]-sum[i-1] < f[i][j]) {
                    f[i][j] = f[i][l]+f[l+1][j] + sum[j]-sum[i-1] ; 
                    s[i][j] = l ; 
                }
            }
        if(d == n) minn = min(f[i][j] , minn) , maxn = max(p[i][j] , maxn) ; 
        }
    }
    cout << minn << endl << maxn << endl ; 
    return 0 ; 
}

  

教程转载

P1880 [NOI1995]石子合并

原文：https://www.cnblogs.com/trouble-faker/p/10397167.html