六、时间差分方法
1.给定一个策略,如何估算其值函数?在蒙特卡洛方法中,智能体以阶段形式与环境互动,一个阶段结束后,我们按顺序查看每个状态动作对,如果是首次经历,则计算相应的回报并使用它来更新动作值。我们经历了很多很多个阶段。需要注意的是,只要我们不在阶段之间更改策略,该算法就可以解决预测问题,只要我们运行该算法足够长的时间,就肯定能够获得一个很完美的动作值函数估计结果:

2.现在将重点转移到这个更新步骤:
![]()
这行的主要原理是,任何状态的值定义为智能体遵守策略后在该状态之后很可能会出现的预期回报,对取样回报取平均值生成了很好的估值。回想下关于状态值的贝尔曼预期方程,它可以使用潜在地跟在后面的状态的值表示任何状态的值:
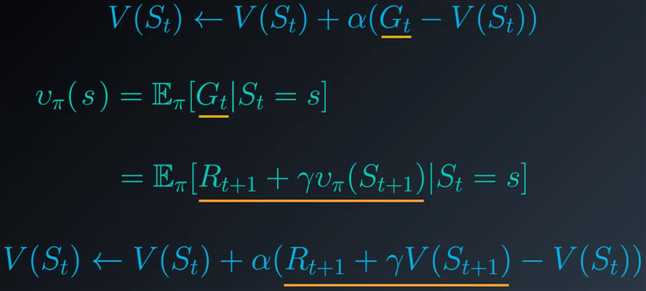
现在我们不再对取样回报取平均值,而是根据后续状态的值来估算,这就使得我们能够在每个时间步之后更新状态值。
3.改写上述方程式:

我们需要在当前估值和TD目标之间做一个平衡。α 必须设为 0 和 1 之间的某个数字。当 α 设为 1 时,新的估值是 TD 目标,我们完全忽略并替换之前的估值,如果将 α 设为 0,则完全忽略目标并保留旧的估值,我们肯定不希望出现这种结果,因为智能体将无法学到规律。将 α 设为一个接近 0 的小值很有帮助,通常 α 越小,我们在进行更新时对目标的信任就越低,并且更加依赖于状态值的现有估值。
4.TD算法的伪代码:

TD(0) 保证会收敛于真状态值函数,只要步长参数 α 足够小。MC 预测也是这种情况。但是,TD(0) 具有一些优势:
在阶段性任务中使用TD(0),只需检查在每个时间步,最近的状态是否为最终状态,如果是,我们最后一次运行更新步骤以便更新上一个状态,然后开始一个新的阶段。
机器学习工程师 - Udacity 强化学习 Part Five
原文:https://www.cnblogs.com/paulonetwo/p/10415189.html