* 问题描述:
设要传输由 n 种基本字符构成的一段信息。已知每种字符在信息中出现的频次 w[i], 1 ≤ i ≤ n (即第 i 种字符在一段信息中出现 w[i] 次)。现在要对这 n 种字符构造一种不等长无歧义的 k 进制前缀编码,使得传输该段信息的编码总长度最短。求该最短长度。
* 基本思路:
一般算法课都会介绍Huffman编码,它就是该问题在 k = 2 下的一种特例。自然的,会想到用类似Huffman算法来解决该问题。
一种典型的错误:
相信有些同志一开始会直接“无脑”地将Huffman算法中的 2 改成 k,即:首先把 n 个结点依次放入一个小顶堆(频次 w 最小的结点位于堆顶);然后不断地依次从堆顶取出 k 个结点“捏”在一起构成一个新结点,新结点权重为 k 个子结点之和,并将其放回堆中。当堆中的结点数 ≤ k 时,合并成Huffman树的根节点,算法结束。
这种算法有一个致命的问题,即这样做生成的树根结点的孩子可能不满 k 个,这显然不是最短的编码方案。因为把任一非根结点孩子的叶节点改为根结点的孩子后得到的编码长度一定更短。如下图所示。
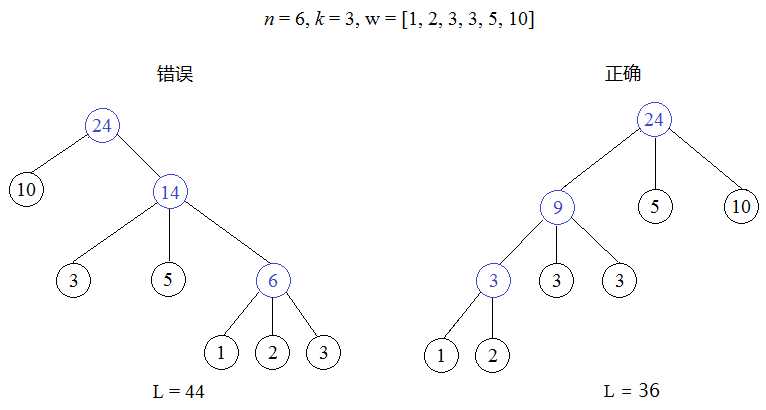
* C++示例代码:
1 #include <cstdio> 2 #include <queue> 3 #include <functional> 4 using namespace std; 5 6 const int MAXN = 300000; // 最大单词种类数 7 int weights[MAXN]; // 存储各单词的权重 8 long long kHuffman(int n, int k, int * weights); /* 返回k重Huffman编码长度 */ 9 10 int main() 11 { 12 int n, k; // 单词种类数,用k进制串进行编码 13 scanf("%d %d", &n, &k); 14 for ( int i = 0; i < n; ++i ) 15 scanf("%d", weights+i); 16 printf("%lld\n", kHuffman(n, k, weights)); 17 return 0; 18 } 19 20 long long kHuffman(int n, int k, int * weights) 21 { 22 /* 平凡情况 */ 23 if ( n == 0 ) 24 return 0; 25 if ( n == 1 ) 26 return 1; 27 28 /* k重前缀码 */ 29 long long length = 0; 30 priority_queue<long long, vector<long long>, greater<long long> > q; 31 32 for ( int i = 0; i < n; ++i ) 33 q.push(weights[i]); 34 int r = (n - 1) % (k - 1); 35 if ( r ) 36 for ( int i = 0; i < k-1-r; ++i ) 37 q.push(0); 38 39 while ( q.size() > 1 ) 40 { 41 long long v = 0; 42 for ( int i = 0; i < k; ++i ) 43 { 44 v += q.top(); 45 q.pop(); 46 } 47 q.push(v); 48 length += v; 49 } 50 51 return length; 52 }
原文:https://www.cnblogs.com/fyqq0403/p/10422495.html