Pseudo-Random Numbers
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1064 Accepted Submission(s): 460
Problem Description
Computers normally cannot generate really random numbers, but frequently are used to generate sequences of pseudo-random numbers. These are generated by some algorithm, but appear for all practical purposes to be really random. Random numbers are used in many applications, including simulation.
A common pseudo-random number generation technique is called the linear congruential method. If the last pseudo-random number generated was L, then the next number is generated by evaluating ( Z x L + I ) mod M, where Z is a constant multiplier, I is a constant increment, and M is a constant modulus. For example, suppose Z is 7, I is 5, and M is 12. If the first random number (usually called the seed) is 4, then we can determine the next few pseudo-random numbers are follows:
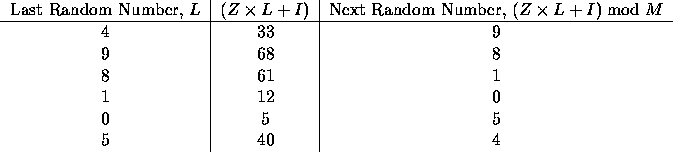
As you can see, the sequence of pseudo-random numbers generated by this technique repeats after six numbers. It should be clear that the longest sequence that can be generated using this technique is limited by the modulus, M.
In this problem you will be given sets of values for Z, I, M, and the seed, L. Each of these will have no more than four digits. For each such set of values you are to determine the length of the cycle of pseudo-random numbers that will be generated. But be careful: the cycle might not begin with the seed!
Input
Each input line will contain four integer values, in order, for Z, I, M, and L. The last line will contain four zeroes, and marks the end of the input data. L will be less than M.
Output
For each input line, display the case number (they are sequentially numbered, starting with 1) and the length of the sequence of pseudo-random numbers before the sequence is repeated.
Sample Input
7 5 12 4
5173 3849 3279 1511
9111 5309 6000 1234
1079 2136 9999 1237
0 0 0 0
Sample Output
Case 1: 6
Case 2: 546
Case 3: 500
Case 4: 220
Source
North Central North America 1996
Regionals 1996 >> North America - North Central NA
问题链接:HDU1324 ZOJ1278 UVA350 UVALive5458 Pseudo-Random Numbers
问题简述:
给定Z, I, M, L,由随机数产生式k=(Z*L+I)%M产生随机数,其中L表示上一个随机数。那么就会有随机数序列,并且会产生循环,计算循环的长度。
问题分析:
????使用迭代计算即可,如果计数到L重复出现,就算出了循环长度。
程序说明:(略)
参考链接:(略)
题记:(略)
AC的C++语言程序如下:
/* HDU1324 ZOJ1278 UVA350 UVALive5458 Pseudo-Random Numbers */
#include <bits/stdc++.h>
using namespace std;
const int N = 10000 + 1;
bool ans[N];
int num[N];
int main()
{
int z, i, m, l, caseno = 0;
while(~scanf("%d%d%d%d", &z, &i, &m, &l) && (z || i || m || l)) {
memset(ans, 0, sizeof(ans));
memset(num, 0, sizeof(num));
int cur = l, cnt = 1;
ans[cur] = true;
num[cur] = 1;
for(;;) {
cur = (z * cur + i) % m;
if(ans[cur]) {
printf("Case %d: %d\n", ++caseno, cnt - num[cur] + 1);
break;
}
ans[cur] = 1; // 标记
num[cur] = ++cnt; // 步数
}
}
return 0;
}HDU1324 ZOJ1278 UVA350 UVALive5458 Pseudo-Random Numbers【模除+随机函数】
原文:https://www.cnblogs.com/tigerisland45/p/10425617.html