AVL树,即平衡二叉搜索树,并且其左右子树的高度相差小于等于1。
AVL树的实现,在于插入节点的同时,保持树的平衡性。共分为如下四种旋转:
1. 左单边右旋转
当在k1的左子树上插入节点以后,导致K2失去平衡后的旋转。
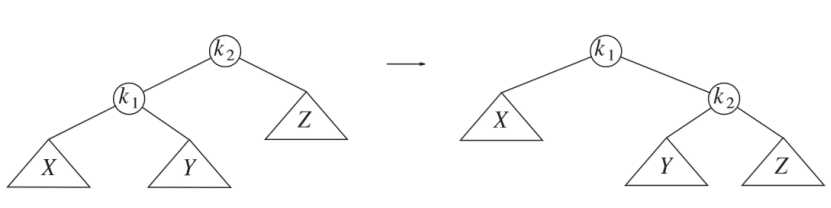
代码实现如下:
/* * * 左单边向右旋转 */ void singleRotateWithLeft(AvlNode * & k2) { AvlNode * k1 = k2->left; k2->left = k1->right; k1->right = k2; k2->h = max(h(k2->left), h(k2->right)) + 1; k1->h = max(h(k1->left), h(k1->right)) + 1; k2 = k1; }
2. 右单边左旋转
当在K2点右子树上插入节点后,导致的旋转,如下图;
代码如下:
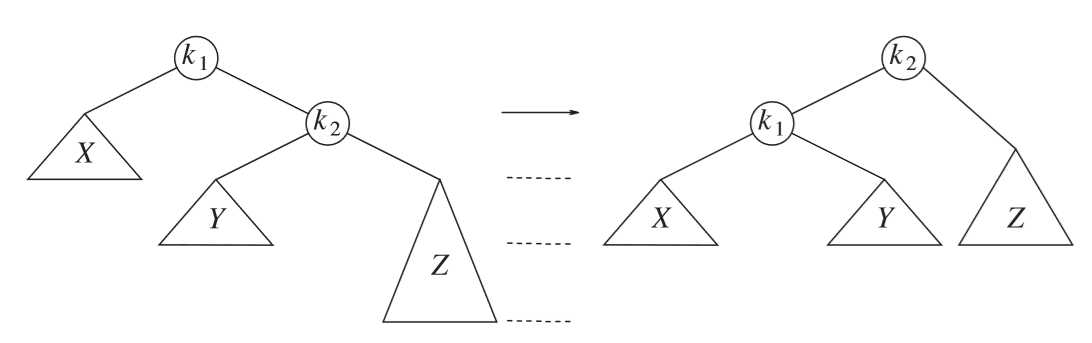
代码如下:
/* * * 右单边向左旋转 * */ void singleRotateWithRight(AvlNode * & k1) { AvlNode * k2 = k1->right; k1->right = k2->left; k2->left = k1; k1->h = max(h(k1->left), h(k1->right)) + 1; k2->h = max(h(k2->left), h(k2->right)) + 1; k1 = k2; }
3. 左边2次旋转:
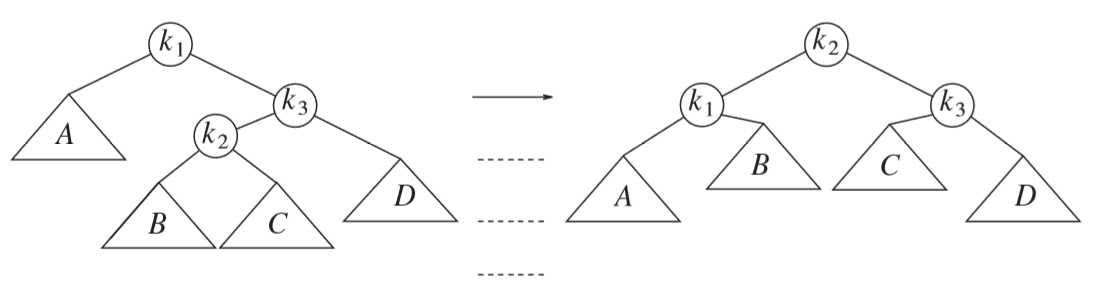
当在K1的右子树上插入节点,导致K3失去平衡后的旋转。此时,需要做2次旋转。
a. 以K1为根,进行右单边左旋转
b. 以K3为根,进行左单边右旋转

代码如下:
/* * * 左单边向右doube旋转 */ void doubleRotateWithLeft(AvlNode * & node) { singleRotateWithRight(node->left); singleRotateWithLeft(node); }
4. 右边2次旋转
代码
/* * * 右单边向左doube旋转 */ void doubleRotateWithRight(AvlNode * & node) { singleRotateWithLeft(node->right); singleRotateWithRight(node); }
all code :
class MyAVLTree { private: struct AvlNode { int val; AvlNode * left; AvlNode * right; int h; AvlNode(int x) : val(x), h(0), left(NULL), right(NULL) {} }; AvlNode * root; static const int ALLOWED_IMBALANCE = 1; public: MyAVLTree():root(NULL) {} AvlNode * getHead() { return root; } int h(AvlNode * root) { return root == NULL ? 0 : root->h; } void insert(int value) { insert(value, root); } void insert(int value,AvlNode * & node) { if (node == NULL) { node = new AvlNode{value}; } else if (value < node->val) { insert(value, node->left); } else if (value > node->val) { insert(value, node->right); } balance(node); } void balance(AvlNode * & node) { if (node == NULL) { return; } if (h(node->left) - h(node->right) > ALLOWED_IMBALANCE) { if (h(node->left->left) >= h(node->left->right)) { singleRotateWithLeft(node); } else { doubleRotateWithLeft(node); } } else if (h(node->right) - h(node->left) > ALLOWED_IMBALANCE) { if (h(node->right->right) >= h(node->right->left)) { singleRotateWithRight(node); } else { doubleRotateWithRight(node); } } node->h = max(h(node->left), h(node->right)) + 1; } /* * * 左单边向右旋转 k2 k1 k1 z ==> x k2 x y y z */ void singleRotateWithLeft(AvlNode * & k2) { AvlNode * k1 = k2->left; k2->left = k1->right; k1->right = k2; k2->h = max(h(k2->left), h(k2->right)) + 1; k1->h = max(h(k1->left), h(k1->right)) + 1; k2 = k1; } /* * * 右单边向左旋转 * k1 k2 * x k2 ==> k1 z * y z x y * * */ void singleRotateWithRight(AvlNode * & k1) { AvlNode * k2 = k1->right; k1->right = k2->left; k2->left = k1; k1->h = max(h(k1->left), h(k1->right)) + 1; k2->h = max(h(k2->left), h(k2->right)) + 1; k1 = k2; } /* * * 左单边向右doube旋转 */ void doubleRotateWithLeft(AvlNode * & node) { singleRotateWithRight(node->left); singleRotateWithLeft(node); } /* * * 右单边向左doube旋转 */ void doubleRotateWithRight(AvlNode * & node) { singleRotateWithLeft(node->right); singleRotateWithRight(node); } int max(int a, int b) { return a > b ? a : b; } void printAvlTreeWithPreOder(AvlNode * node) { if (node == NULL) { return; } cout << node->val << " "; printAvlTreeWithPreOder(node->left); printAvlTreeWithPreOder(node->right); } void printAvlTreeWithInOder(AvlNode * node) { if (node == NULL) { return; } printAvlTreeWithInOder(node->left); cout << node->val << " "; printAvlTreeWithInOder(node->right); } };
原文:https://www.cnblogs.com/ordili/p/10432596.html