PCA主成分分析,无监督学习降维方法:
import matplotlib.pyplot as plt import matplotlib.image as maping import matplotlib import numpy as np import seaborn as sns import pandas as pds import plotly.graph_objs as go import plotly.tools as tls %matplotlib inline from sklearn.manifold import TSNE from sklearn.decomposition import PCA from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
使用sklearn方式展现PCA
train=pds.read_csv("train.csv") train.head()
| label | pixel0 | pixel1 | pixel2 | pixel3 | pixel4 | pixel5 | pixel6 | pixel7 | pixel8 | pixel9 | pixel10 | pixel11 | pixel12 | pixel13 | pixel14 | pixel15 | pixel16 | pixel17 | pixel18 | pixel19 | pixel20 | pixel21 | pixel22 | pixel23 | pixel24 | pixel25 | pixel26 | pixel27 | pixel28 | pixel29 | pixel30 | pixel31 | pixel32 | pixel33 | pixel34 | pixel35 | pixel36 | pixel37 | pixel38 | pixel39 | pixel40 | pixel41 | pixel42 | pixel43 | pixel44 | pixel45 | pixel46 | pixel47 | pixel48 | pixel49 | pixel50 | pixel51 | pixel52 | pixel53 | pixel54 | pixel55 | pixel56 | pixel57 | pixel58 | ... | pixel724 | pixel725 | pixel726 | pixel727 | pixel728 | pixel729 | pixel730 | pixel731 | pixel732 | pixel733 | pixel734 | pixel735 | pixel736 | pixel737 | pixel738 | pixel739 | pixel740 | pixel741 | pixel742 | pixel743 | pixel744 | pixel745 | pixel746 | pixel747 | pixel748 | pixel749 | pixel750 | pixel751 | pixel752 | pixel753 | pixel754 | pixel755 | pixel756 | pixel757 | pixel758 | pixel759 | pixel760 | pixel761 | pixel762 | pixel763 | pixel764 | pixel765 | pixel766 | pixel767 | pixel768 | pixel769 | pixel770 | pixel771 | pixel772 | pixel773 | pixel774 | pixel775 | pixel776 | pixel777 | pixel778 | pixel779 | pixel780 | pixel781 | pixel782 | pixel783 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
print(train.shape)
target=train["label"] train=train.drop("label",axis=1) train.head()
| pixel0 | pixel1 | pixel2 | pixel3 | pixel4 | pixel5 | pixel6 | pixel7 | pixel8 | pixel9 | pixel10 | pixel11 | pixel12 | pixel13 | pixel14 | pixel15 | pixel16 | pixel17 | pixel18 | pixel19 | pixel20 | pixel21 | pixel22 | pixel23 | pixel24 | pixel25 | pixel26 | pixel27 | pixel28 | pixel29 | pixel30 | pixel31 | pixel32 | pixel33 | pixel34 | pixel35 | pixel36 | pixel37 | pixel38 | pixel39 | pixel40 | pixel41 | pixel42 | pixel43 | pixel44 | pixel45 | pixel46 | pixel47 | pixel48 | pixel49 | pixel50 | pixel51 | pixel52 | pixel53 | pixel54 | pixel55 | pixel56 | pixel57 | pixel58 | pixel59 | ... | pixel724 | pixel725 | pixel726 | pixel727 | pixel728 | pixel729 | pixel730 | pixel731 | pixel732 | pixel733 | pixel734 | pixel735 | pixel736 | pixel737 | pixel738 | pixel739 | pixel740 | pixel741 | pixel742 | pixel743 | pixel744 | pixel745 | pixel746 | pixel747 | pixel748 | pixel749 | pixel750 | pixel751 | pixel752 | pixel753 | pixel754 | pixel755 | pixel756 | pixel757 | pixel758 | pixel759 | pixel760 | pixel761 | pixel762 | pixel763 | pixel764 | pixel765 | pixel766 | pixel767 | pixel768 | pixel769 | pixel770 | pixel771 | pixel772 | pixel773 | pixel774 | pixel775 | pixel776 | pixel777 | pixel778 | pixel779 | pixel780 | pixel781 | pixel782 | pixel783 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
#数据标准化 from sklearn.preprocessing import StandardScaler
X=train.values transform=StandardScaler() X_std=transform.fit_transform(X) c:\users\lenovo\appdata\local\programs\python\python36\lib\site-packages\sklearn\utils\validation.py:595: DataConversionWarning: Data with input dtype int64 was converted to float64 by StandardScaler. c:\users\lenovo\appdata\local\programs\python\python36\lib\site-packages\sklearn\utils\validation.py:595: DataConversionWarning: Data with input dtype int64 was converted to float64 by StandardScaler.
#特征向量和特征值 mean_vec=np.mean(X_std,axis=0) cov_mat=np.cov(X_std.T) eig_vals,eig_vecs=np.linalg.eig(cov_mat) #创建特征向量和特征值的元组 eig_pairs=[(np.abs(eig_vals[i]),eig_vecs[:,i] for i in range(len(eig_vals))] #对特征向量和特征值进行排序 eig_pairs.sort(key=lambda x : x[0],reverse=True) #计算累计解释方差 tot=sum(eig_vals) var_exp=[(i/tot)*100 for i in sorted(eig_vals,reverse=True)] cum_var_exp=np.cumsum(var_exp)
#接下来使用Ploty可视化显示 trace1=go.Scatter(x=list(range(784)),y=cum_var_exp,mode="lines+markers",name="‘累计解释方差‘",line=dict(shape=‘spline‘,color=‘goldenrod‘)) trace2=go.Scatter(x=list(range(784)),y=var_exp,mode="lines+markers",name="‘单个解释方差‘",line=dict(shape=‘linear‘,color=‘black‘)) fig=tls.make_subplots(insets=[{‘cell‘:(1,1),‘l‘:0.7,‘b‘:0.5}],print_grid=True) fig.append_trace(trace1,1,1) fig.append_trace(trace2,1,1) fig.layout.title="解释方差" fig.layout.xaxis=dict(range=[0,80],title="特征列") fig.layout.yaxis=dict(range=[0,60],title="解释变量")
This is the format of your plot grid: [ (1,1) x1,y1 ] With insets: [ x2,y2 ] over [ (1,1) x1,y1 ]
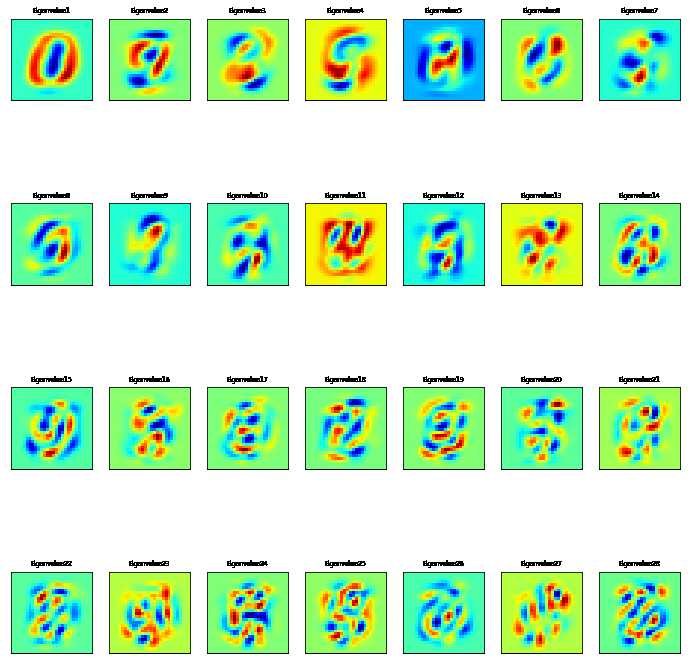
#可视化特征值 n_components=30 pca=PCA(n_components=n_components).fit(train.values) eigenvalues=pca.components_.reshape(n_components,28,28) eigenvalues=pca.components_
n_row=4 n_col=7 #显示前8个特征值 plt.figure(figsize=(12,13)) for i in list(range(n_row*n_col)): offset=0 plt.subplot(n_row,n_col,i+1) plt.imshow(eigenvalues[i].reshape(28,28),cmap=‘jet‘) title_text="Eigenvalue"+str(i+1) plt.title(title_text,size=6.5) plt.xticks(()) plt.yticks(()) plt.show()
plt.figure(figsize=(14,12)) for digit_num in range(0,70): plt.subplot(7,10,digit_num+1) grid_data=train.iloc[digit_num].as_matrix().reshape(28,28) plt.imshow(grid_data,interpolation="none",cmap="afmhot") plt.xticks([]) plt.yticks([]) plt.tight_layout()
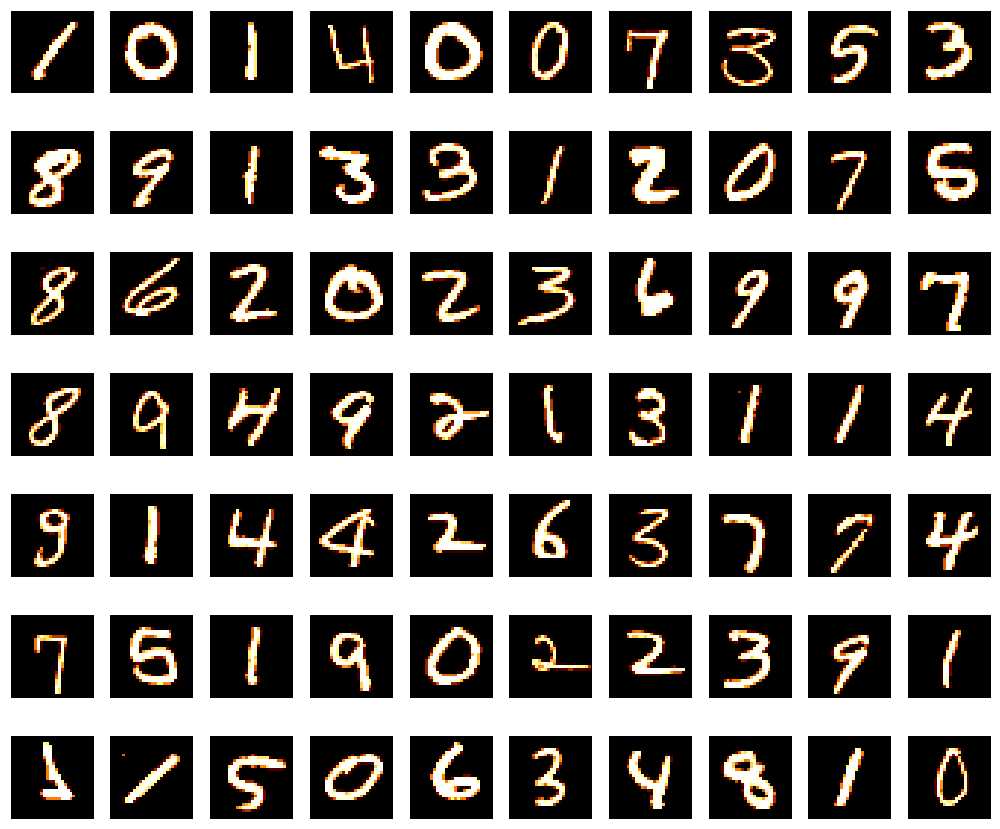
#PCA使用在SK-learn中 del X X=train[:6000].values del train X_std=StandardScaler().fit_transform(X) pca=PCA(n_components=5) pca.fit(X_std) X_5d=pca.transform(X_std)
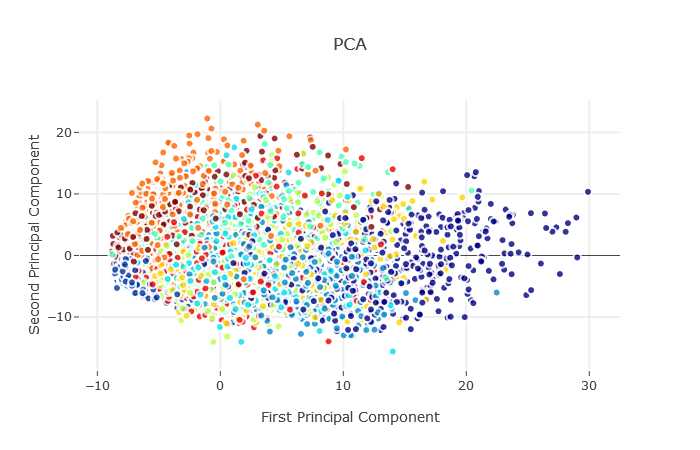
#使用散点图显示PCA效果 import plotly.offline as py py.offline.init_notebook_mode(connected=True) Target=target[:6000] trace0=go.Scatter(x=X_5d[:,0],y=X_5d[:,1],mode="markers",text=Target,showlegend=False,marker=dict(size=8,color=Target,colorscale="Jet",showscale=False,line=dict(width=2,color="rgb(255,255,255)"),opacity=0.8)) data=[trace0] layout=go.Layout(title="PCA",hovermode="closest",xaxis=dict(title="First Principal Component",ticklen=5,zeroline=False,gridwidth=2,),yaxis=dict(title="Second Principal Component",ticklen=5,gridwidth=2,),showlegend=True) fig=dict(data=data,layout=layout) py.iplot(fig,filename="style-scatter")
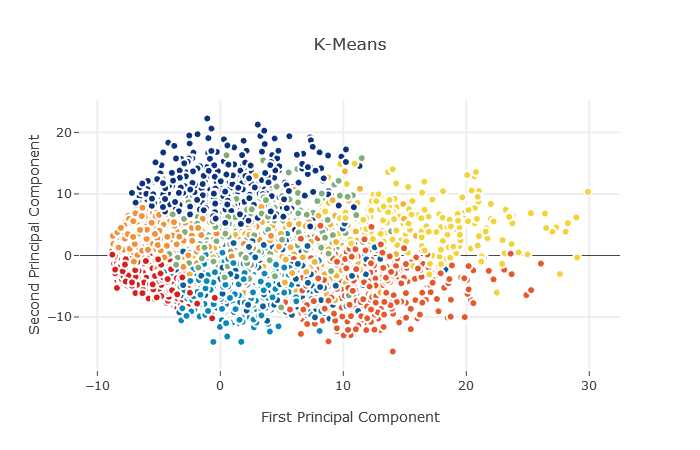
from sklearn.cluster import KMeans kmeans=KMeans(n_clusters=9) X_clustered=kmeans.fit_predict(X_5d) trace_Kmeans=go.Scatter(x=X_5d[:,0],y=X_5d[:,1],mode="markers",showlegend=False,marker=dict(size=8,color=X_clustered,colorscale="Portland",showscale=False,line=dict(width=2,color=‘rgb(255,255,255)‘)))
layout=go.Layout(title="K-Means",hovermode="closest",xaxis=dict(title="First Principal Component",ticklen=5,zeroline=False,gridwidth=2,),yaxis=dict(title="Second Principal Component",ticklen=5,gridwidth=2,),showlegend=True) data=[trace_Kmeans] fig1=dict(data=data,layout=layout) py.iplot(fig1,filename="svm")
原文:https://www.cnblogs.com/knight-vien/p/10433683.html