1. 关于非线性转化方程(non-linear transformation function)
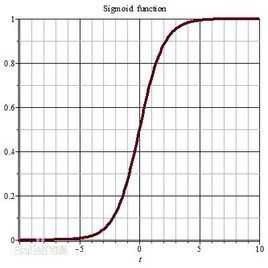
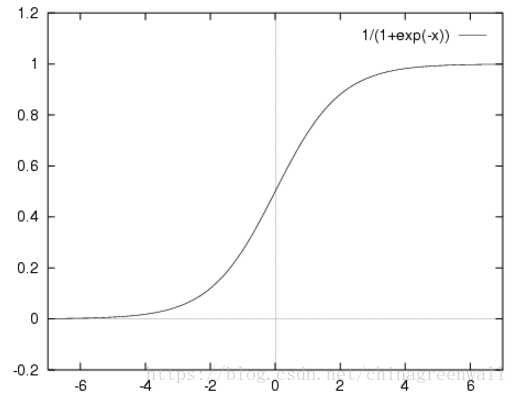
其实logistic函数也就是经常说的sigmoid函数,它的几何形状也就是一条sigmoid曲线(S型曲线)。
导数:
![]()
# -*- coding:utf-8 -*-
import numpy as np
def tanh(x):
return np.tanh(x)
def tanh_deriv(x):
return 1.0 - np.tanh(x) * np.tanh(x)
def logistic(x):
return 1/(1 + np.exp(x))
def logistic_derivative(x):
return logistic(x) * (1 - logistic(x))
class NeuralNetwork:
def __init__(self, layers, activation = ‘tanh‘):
"""
:param layers: A list containing the number of units in each layer.
Should be at least two values
:param activation: The activation function to be used. Can be
"logistic" or "tanh"
"""
if activation == ‘logistic‘:
self.activation = logistic
self.activation_deriv = logistic_derivative
elif activation == ‘tanh‘:
self.activation = tanh
self.activation_deriv = tanh_deriv
self.weights = []
for i in range(1, len(layers) - 1):
self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1 )*0.25)
self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1])) - 1)*0.25)
def fit(self, X, y, learning_rate = 0.2, epochs = 10000): #epochs = 10000 抽样更新 10000次
X = np.atleast_2d(X) #至少2维
temp = np.ones([X.shape[0], X.shape[1] + 1])#初始化矩阵
temp[: ,0:-1] = X # adding the bias unit to the input layer 每一行 从第一列到最后一列 不包含最后一列
X = temp
y = np.array(y)
for k in range(epochs): #第一次循环
i = np.random.randint(X.shape[0]) #X里面随机选取一行
a = [X[i]] #第i行
for l in range(len(self.weights)): #going forward network, for each layer
a.append(self.activation(np.dot(a[l], self.weights[l]))) #Computer the node value for each layer (O_i) using activation function
error = y[i] - a[-1] #Computer the error at the top layer
#对于输出层
deltas = [error * self.activation_deriv(a[-1])] #For output layer, Err calculation (delta is updated error)
# Staring backprobagation
#(len(a) - 2)因为不能算第一层和最后一层;最后一层到0层,倒回去
for l in range(len(a) - 2, 0 ,-1):# we need to begin at the second to last layer
#Compute the updated error (i,e, deltas) for each node going from top layer to input layer
#对于隐藏层
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
deltas.reverse()#0层到最后一层
for i in range(len(self.weights)):#权重更新
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learining_rate * layer.T.dot(delta)
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0] + 1)
temp[0 : -1] = x
a = temp
for l in range(0, len(self.weights)):
a = self.activation(np.dot(a, self.weights[1]))
return a
原文:https://www.cnblogs.com/lyywj170403/p/10433711.html