一般梯度下降:
\[
L=\sum_n(\tilde{y}^n - (b+\sum w_ix_i^n))^2 \w^{t+1}\gets w^t-\eta^tg^t\\eta^t=\frac{\eta}{\sqrt{t+1}}
\]
Adagrad:
\[
w^{t+1}\gets w^t-\frac{\eta^t}{\sigma}g^t\g^t=\frac{\partial L(\theta^t)}{\partial w}\\eta^t = \frac{\eta}{\sqrt{t+1}}\\sigma^t=\sqrt{\frac{1}{t=1}\sum^t_{i=0}(g^i)^2}
\]
化简:
\[
w^{t+1}\gets w^t-\frac{\eta}{\sqrt{\sum^t_{i=0}(g^i)^2}}g^t\\]
两个输入数据分布的范围不一样,差别较大,建议进行缩放处理,使得数据分布的范围一样
数据不进行处理,会导致特征间的影响程度差异大,对于同一个学习率,更新数据偏差大
实际上就是将数据分布由椭圆进行坐标变换,化为同心圆。
常规做法:\[x_i^r \gets \frac{x_i^r - \bar{x}}{\sigma _i},\bar{x}是平均值,\sigma_i是标准差\]
如果\(h(x)在x=x_0\) 点的某个领域内有无限阶导数,则有泰勒级数:
\[
\begin{split}
h(x)&=\sum^\infty_{k=0}\frac{h^k(x_0)}{k!}(x-x_0)^k\&=h(x_0)+h'(x_0)(x-x_0)+\frac{h''(x_0)}{!}(x-x_0)^2+...
\end{split}
\]
二元泰勒:
\[
h(x,y)=h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0)+...
\]
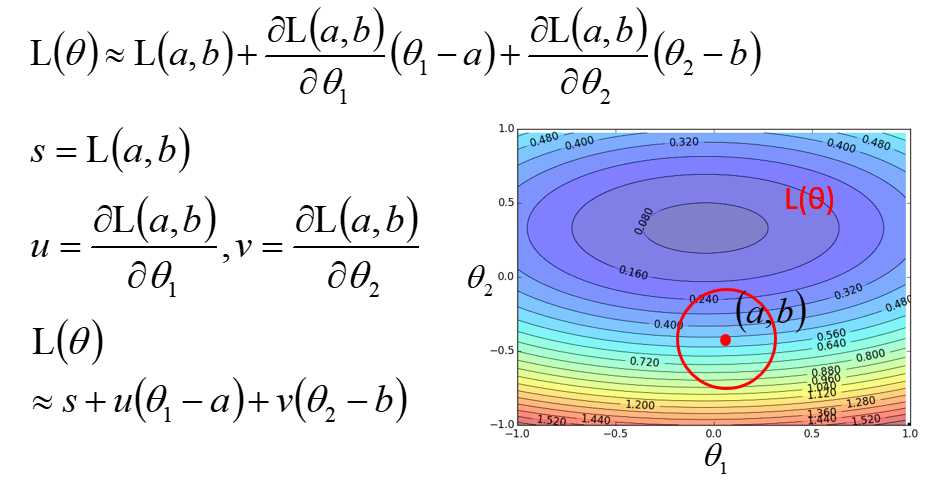
在小范围的圆里面找到最小值,然后不断递归,直到找到全局最小值。
基于泰勒展开式,化简:

两个向量内积如何最小,一定是反向180°即可。因此有:
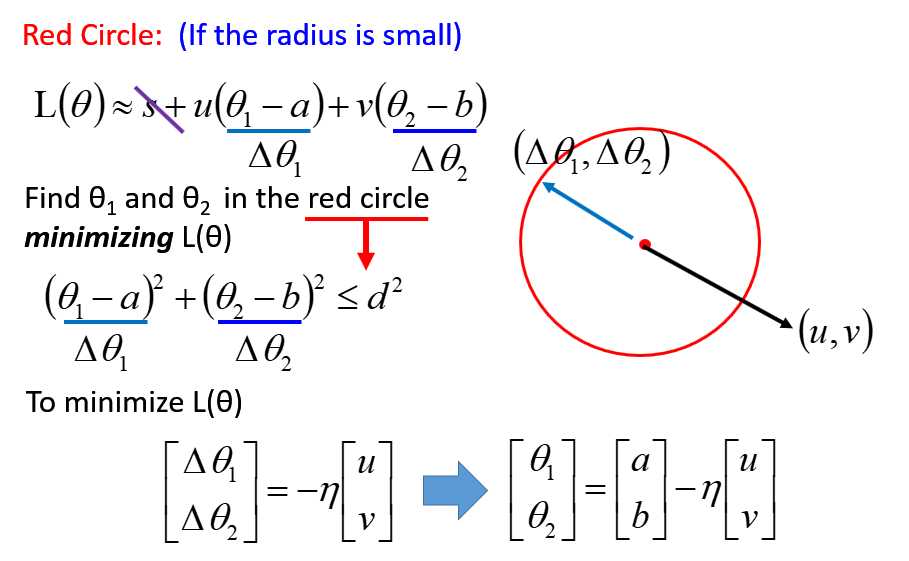
最后有:

原文:https://www.cnblogs.com/niubidexiebiao/p/10446453.html