/*
* 给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
* 输入: "A man, a plan, a canal: Panama"
输出: true
回文串:正读和反读都是一样的字符串。
* */
public boolean isPalindrome2(String s){
// 对初始字符串进行预处理
s=s.toLowerCase();
int low=0;
int high=s.length()-1;
while(low<high){
if(!Character.isLetterOrDigit(s.charAt(low))) low++;
else if(!Character.isLetterOrDigit(s.charAt(high))) high--;
else if(s.charAt(low)!=s.charAt(high)) return false;
else{
low++;
high--;
}
}
return true;
}
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
暴力求解方法:
public int strStr(String haystack, String needle) {
// 暴力解法
if(needle.isEmpty()) return -1;
final int N=haystack.length()-needle.length()+1;
for(int i=0;i<N;i++){
int j=i;
int k=0;
while(j<haystack.length() && k<needle.length() && haystack.charAt(j)==needle.charAt(k)){
k++;
j++;
}
if(k==needle.length()){
return i;
}
}
return -1;
}
/*
* 给定两个二进制字符串,返回他们的和(用二进制表示)。
输入为非空字符串且只包含数字 1 和 0。
* */
public String addBinary(String a, String b) {
StringBuilder result=new StringBuilder();
int i=a.length()-1;
int j=b.length()-1;
int carry=0;
while(i>=0 || j>=0 || carry>0){
int valueA=i<0 ? 0: a.charAt(i--)-‘0‘;
int valueB=j<0 ? 0: b.charAt(j--)-‘0‘;
int sum=valueA+valueB+carry;
result.insert(0, Character.forDigit(sum%2, 10));
carry=sum/2;
}
return result.toString();
}
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
策略:
A:暴力求解:时间复杂度是o(n*2)
B:记忆化搜索:复杂度 O(n^2) 。设 f[i][j] 表示[i,j]之间的最长回文子串,递推方程如下:
f[i][j] = if (i == j) S[i]
if (S[i] == S[j] && f[i+1][j-1] == S[i+1][j-1]) S[i][j]
else max(f[i+1][j-1], f[i][j-1], f[i+1][j])
C:动态规划算法:
设状态为 f(i,j) ,表示区间[i,j]是否为回文串,则状态转移方程为
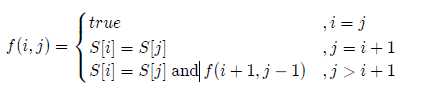
/*
* 动态规划问题经常用于求解最优子结构以及重叠子问题,以前我们经常将重叠子问题
* 使用递归进行实现,但是有问题的是,会进行大量重复的计算,而动态规划就是将之前的结果保存下来,避免了不必要的
* 重复操作,提升了效率。
*
* 实现原理:
* 借助一个二维布尔数组
* 每个dp[i][j]表示一个方格,每个方格中的T与F分别表示当前子串是否是
* 回文字符串。
* 再进行转换的时候,表达式即是str[i]==str[j] && dp[i+1][j-1]
* */
public String longestPalindrome3(String s){
int len=s.length();
int maxlen=0;
String res=null;
boolean [][] dp=new boolean[len][len];
for(int i=len-1;i>=0;i--){
for(int j=i;j<len;j++){
dp[i][j]=s.charAt(i)==s.charAt(j) && (j-i<3 || dp[i+1][j-1]);
if(dp[i][j] && (res==null || j-i+1>maxlen)){
res=s.substring(i,j+1);
maxlen=res.length();
}
}
}
return res;
}
原文:https://www.cnblogs.com/qian2015/p/10451587.html