半平面交&多边形内核。因为没注意了点的情况自闭了。
https://blog.csdn.net/qq_40861916/article/details/83541403
这个说的贼好。
多边形内核就是多边形内部的一块区域/一个点,能看到多边形的任何地方。
怎么求呢。
首先每条边要逆时针。
然后我们对所有的边按照与 +x轴的逆时针夹角进行排序。从小到大。
这之后我们每次用双端队列维护已经求出的多边形。
每加入一条新边的话,我们check一下
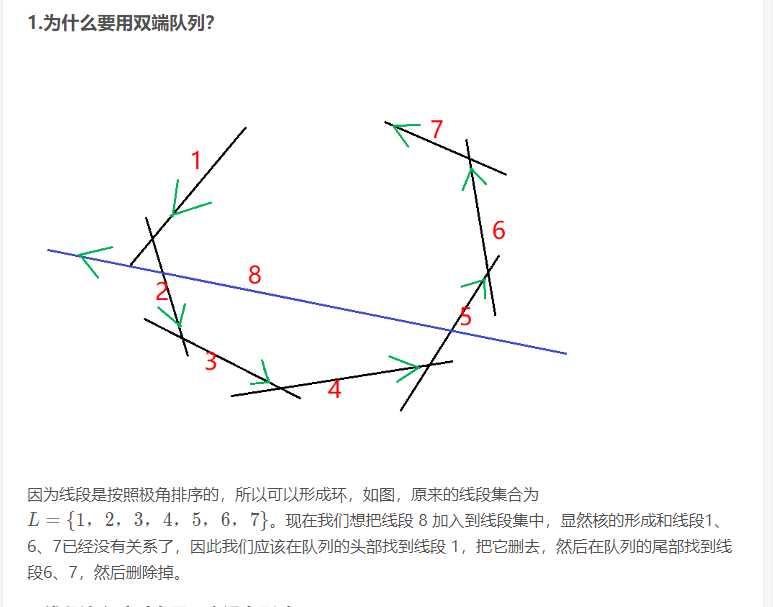
这个图说的太好了!话说这个图的blog我在上面放了链接不算盗用叭。。。
然后就没了。。

1 #include <iostream> 2 #include <cmath> 3 #include <algorithm> 4 #include <cstdio> 5 #include <vector> 6 #include <deque> 7 #define rep(x) for(int i=0;i<x;i++) 8 using namespace std; 9 typedef double db; 10 const db eps=1e-8; 11 const db pi=acos(-1); 12 int sign(db k){ 13 if (k>eps) return 1; else if (k<-eps) return -1; return 0; 14 } 15 int cmp(db k1,db k2){return sign(k1-k2);} 16 int inmid(db k1,db k2,db k3){return sign(k1-k3)*sign(k2-k3)<=0;}// k3 在 [k1,k2] 内 17 struct point{ 18 db x,y; 19 point operator + (const point &k1) const{return (point){k1.x+x,k1.y+y};} 20 point operator - (const point &k1) const{return (point){x-k1.x,y-k1.y};} 21 point operator * (db k1) const{return (point){x*k1,y*k1};} 22 point operator / (db k1) const{return (point){x/k1,y/k1};} 23 int operator == (const point &k1) const{return cmp(x,k1.x)==0&&cmp(y,k1.y)==0;} 24 // 逆时针旋转 25 point turn(db k1){return (point){x*cos(k1)-y*sin(k1),x*sin(k1)+y*cos(k1)};} 26 point turn90(){return (point){-y,x};} 27 bool operator < (const point k1) const{ 28 int a=cmp(x,k1.x); 29 if (a==-1) return 1; else if (a==1) return 0; else return cmp(y,k1.y)==-1; 30 } 31 db abs(){return sqrt(x*x+y*y);} 32 db abs2(){return x*x+y*y;} 33 db dis(point k1){return ((*this)-k1).abs();} 34 point unit(){db w=abs(); return (point){x/w,y/w};} 35 void scan(){double k1,k2; scanf("%lf%lf",&k1,&k2); x=k1; y=k2;} 36 void print(){printf("%.11lf %.11lf\n",x,y);} 37 db getw(){return atan2(y,x);} 38 point getdel(){if (sign(x)==-1||(sign(x)==0&&sign(y)==-1)) return (*this)*(-1); else return (*this);} 39 int getP() const{return sign(y)==1||(sign(y)==0&&sign(x)==-1);} 40 }; 41 int inmid(point k1,point k2,point k3){return inmid(k1.x,k2.x,k3.x)&&inmid(k1.y,k2.y,k3.y);} 42 db cross(point k1,point k2){return k1.x*k2.y-k1.y*k2.x;} 43 db dot(point k1,point k2){return k1.x*k2.x+k1.y*k2.y;} 44 db rad(point k1,point k2){return atan2(cross(k1,k2),dot(k1,k2));} 45 // -pi -> pi 46 int compareangle (point k1,point k2){ 47 return k1.getP()<k2.getP()||(k1.getP()==k2.getP()&&sign(cross(k1,k2))>0); 48 } 49 point proj(point k1,point k2,point q){ // q 到直线 k1,k2 的投影 50 point k=k2-k1; return k1+k*(dot(q-k1,k)/k.abs2()); 51 } 52 point reflect(point k1,point k2,point q){return proj(k1,k2,q)*2-q;} 53 int clockwise(point k1,point k2,point k3){// k1 k2 k3 逆时针 1 顺时针 -1 否则 0 54 return sign(cross(k2-k1,k3-k1)); 55 } 56 int checkLL(point k1,point k2,point k3,point k4){// 求直线 (L) 线段 (S)k1,k2 和 k3,k4 的交点 57 return cmp(cross(k3-k1,k4-k1),cross(k3-k2,k4-k2))!=0; 58 } 59 point getLL(point k1,point k2,point k3,point k4){ 60 db w1=cross(k1-k3,k4-k3),w2=cross(k4-k3,k2-k3); return (k1*w2+k2*w1)/(w1+w2); 61 } 62 int intersect(db l1,db r1,db l2,db r2){ 63 if (l1>r1) swap(l1,r1); if (l2>r2) swap(l2,r2); return cmp(r1,l2)!=-1&&cmp(r2,l1)!=-1; 64 } 65 int checkSS(point k1,point k2,point k3,point k4){ 66 return intersect(k1.x,k2.x,k3.x,k4.x)&&intersect(k1.y,k2.y,k3.y,k4.y)&& 67 sign(cross(k3-k1,k4-k1))*sign(cross(k3-k2,k4-k2))<=0&& 68 sign(cross(k1-k3,k2-k3))*sign(cross(k1-k4,k2-k4))<=0; 69 } 70 db disSP(point k1,point k2,point q){ 71 point k3=proj(k1,k2,q); 72 if (inmid(k1,k2,k3)) return q.dis(k3); else return min(q.dis(k1),q.dis(k2)); 73 } 74 db disSS(point k1,point k2,point k3,point k4){ 75 if (checkSS(k1,k2,k3,k4)) return 0; 76 else return min(min(disSP(k1,k2,k3),disSP(k1,k2,k4)),min(disSP(k3,k4,k1),disSP(k3,k4,k2))); 77 } 78 int onS(point k1,point k2,point q){return inmid(k1,k2,q)&&sign(cross(k1-q,k2-k1))==0;} 79 struct circle{ 80 point o; db r; 81 void scan(){o.scan(); scanf("%lf",&r);} 82 int inside(point k){return cmp(r,o.dis(k));} 83 }; 84 struct line{ 85 // p[0]->p[1] 86 point p[2]; 87 line(point k1,point k2){p[0]=k1; p[1]=k2;} 88 point& operator [] (int k){return p[k];} 89 int include(point k){return sign(cross(p[1]-p[0],k-p[0]))>=0;}//非严格包含。 90 point dir(){return p[1]-p[0];} 91 line push(){ // 向外 ( 左手边 ) 平移 eps 92 const db eps = 1e-6; 93 point delta=(p[1]-p[0]).turn90().unit()*eps; 94 return {p[0]-delta,p[1]-delta}; 95 } 96 }; 97 point getLL(line k1,line k2){return getLL(k1[0],k1[1],k2[0],k2[1]);} 98 int parallel(line k1,line k2){return sign(cross(k1.dir(),k2.dir()))==0;} 99 int sameDir(line k1,line k2){return parallel(k1,k2)&&sign(dot(k1.dir(),k2.dir()))==1;} 100 int operator < (line k1,line k2){ 101 if (sameDir(k1,k2)) return k2.include(k1[0]); 102 return compareangle(k1.dir(),k2.dir()); 103 } 104 int checkpos(line k1,line k2,line k3){return k3.include(getLL(k1,k2));} 105 vector<line> getHL(vector<line> &L){ // 求半平面交 , 半平面是逆时针方向 , 输出按照逆时针 106 sort(L.begin(),L.end()); deque<line> q; 107 for (int i=0;i<(int)L.size();i++){ 108 if (i&&sameDir(L[i],L[i-1])) continue; 109 while (q.size()>1&&!checkpos(q[q.size()-2],q[q.size()-1],L[i])) q.pop_back(); 110 while (q.size()>1&&!checkpos(q[1],q[0],L[i])) q.pop_front(); 111 q.push_back(L[i]); 112 } 113 while (q.size()>2&&!checkpos(q[q.size()-2],q[q.size()-1],q[0])) q.pop_back(); 114 while (q.size()>2&&!checkpos(q[1],q[0],q[q.size()-1])) q.pop_front(); 115 vector<line>ans; for (int i=0;i<q.size();i++) ans.push_back(q[i]); 116 return ans; 117 } 118 int t,n; 119 point p[10005]; 120 bool cw(){//时针 121 db s=0; 122 for(int i=1;i<n-1;i++){ 123 s+=cross(p[i]-p[0],p[i+1]-p[0]); 124 } 125 return s>0; 126 } 127 vector<line> l; 128 int main(){ 129 scanf("%d",&t); 130 while (t--){ 131 scanf("%d",&n); 132 rep(n) scanf("%lf%lf",&p[i].x,&p[i].y); 133 if(!cw())reverse(p,p+n); 134 for(int i=0;i<n;i++){ 135 l.push_back(line(p[i],p[(i+1)%n])); 136 } 137 l=getHL(l); 138 if(l.size()>=3){ 139 printf("YES\n"); 140 } else{ 141 printf("NO\n"); 142 } 143 l.clear(); 144 } 145 } 146 /** 147 1 148 17 149 2 -1 2 -2 1 -2 0 -1 -1 -2 -2 -2 -2 -1 -1 0 -2 1 -2 2 -1 2 0 1 1 2 3 2 3 1 2 1 1 0 150 151 */
原文:https://www.cnblogs.com/MXang/p/10452635.html