In mathematics, the nth harmonic number is the sum of the reciprocals of the first n natural numbers:
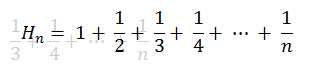
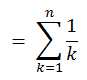
In this problem, you are given n, you have to find Hn.
Input
Input starts with an integer T (≤ 10000), denoting the number of test cases.
Each case starts with a line containing an integer n (1 ≤ n ≤ 108).
Output
For each case, print the case number and the nth harmonic number. Errors less than 10-8 will be ignored.
Sample Input
12
1
2
3
4
5
6
7
8
9
90000000
99999999
100000000
Sample Output
Case 1: 1
Case 2: 1.5
Case 3: 1.8333333333
Case 4: 2.0833333333
Case 5: 2.2833333333
Case 6: 2.450
Case 7: 2.5928571429
Case 8: 2.7178571429
Case 9: 2.8289682540
Case 10: 18.8925358988
Case 11: 18.9978964039
Case 12: 18.9978964139
题意:求f(n)=1/1+1/2+1/3+1/4…1/n (1 ≤ n ≤ 108).,精确到10^-8。
题解:当n很小时,可直接求出结果,当n很大时,利用公式f(n)=ln(n)+C+1/(2*n),在C++ math库中,log即为ln;
代码:

#include <iostream> #include <cstdio> #include <cmath> using namespace std; const double r=0.57721566490153286060651209;//欧拉常数 double a[10000]; int main() { a[1]=1; for (int i=2;i<10000;i++){//预先把小于10000的f(n)求出来 a[i]=a[i-1]+1.0/i; } int n; cin>>n; for (int kase=1;kase<=n;kase++) { cin>>n; if (n<10000){//n<10000时,可直接得出结果 printf("Case %d: %.10lf\n",kase,a[n]); } else{//否则利用欧拉公式 double a=log(n)+r+1.0/(2*n); printf("Case %d: %.10lf\n",kase,a); } } return 0; }
原文:https://www.cnblogs.com/LJHAHA/p/10453043.html