汉诺塔问题是一个经典问题。
题意理解:有A,B,C三个柱子,将A柱子上的N个盘子(从小到大排列)移到C柱子上,每次只允许移动一个盘子,并且保证每个柱子上的盘子的排列都是从小到大。

分析:由题意可知,如果要将A上的盘子移动到C,那么肯定需要借助C。
首先将A上的盘子从上到下依次编号为1-n。
运用整体思想:
1、假设1到n-1个盘子是一个整体
2、将1到n-1个盘子构成的整体移动到B
3、将第n个盘子移动到C
4、再将第2步移动到B的整体移动到C就可以了。
重复以上过程,显然这是一个递归的过程。下面给出代码。
1 public class a2_1_6 { 2 static void Hanoi(int n,char A,char B,char C) //将A上的盘子移动到C 3 { 4 if(n>0){ 5 Hanoi(n-1,A,C,B); //1、将A上1到n-1个盘子移动到B 6 move(A,C);//2、将A最下面那个第n个盘子移动到C 7 Hanoi(n-1,B,A,C); //3、将B上的1到n-1个盘子移动到C 8 } 9 } 10 11 private static void move(char a, char b) { 12 System.out.println(a+"-> "+b); //第二步,将A上剩余的一个盘移到C; 13 } 14 15 public static void main(String args[]){ 16 Hanoi(4,‘A‘,‘B‘,‘C‘); 17 } 18 }
结果大概这么回事:
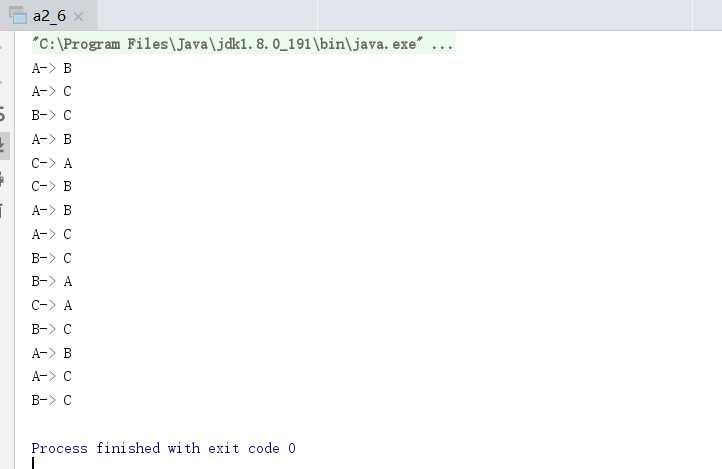
递归写代码很简洁,但是很容易写错,写错基本就StackOverflowError了,然后递归也比较抽象,不是那么容易理解。所以我的原则是可以不用递归尽量不用,后面有时间找找非递归版本的汉诺塔。本人学渣,不足之处,望各位大佬指正,谢谢!
原文:https://www.cnblogs.com/woyaodangxueba/p/10453067.html