排序使程序开发中一种常见的操作。将一组杂乱无章的数据按一定的规则将其排列好。使数据得以快速检索到,这就是排序的目的。
对于一个排序算法,一般可以从下面三个方面去衡量算法的优劣:
1) 时间复杂度:主要缝隙关键字的比较次数和移动字数;
2) 空间复杂度:缝隙排序算法中需要多少辅助内存;
3) 稳定性:当两个关键字相同,如果排序完成后两者的顺序保持不变,则是该排序算法是稳定。
排序算法大致可以分为内部算法和外部算法。如果整个排序过程不需要借助于外部储存器(磁盘),所有的操作都在内存中完成,则称之为内部算法。如果参与排序树数据元素非常多,数据量非常大,则计算机必须借助外部储存器(如磁盘),这种排序称为外部排序。
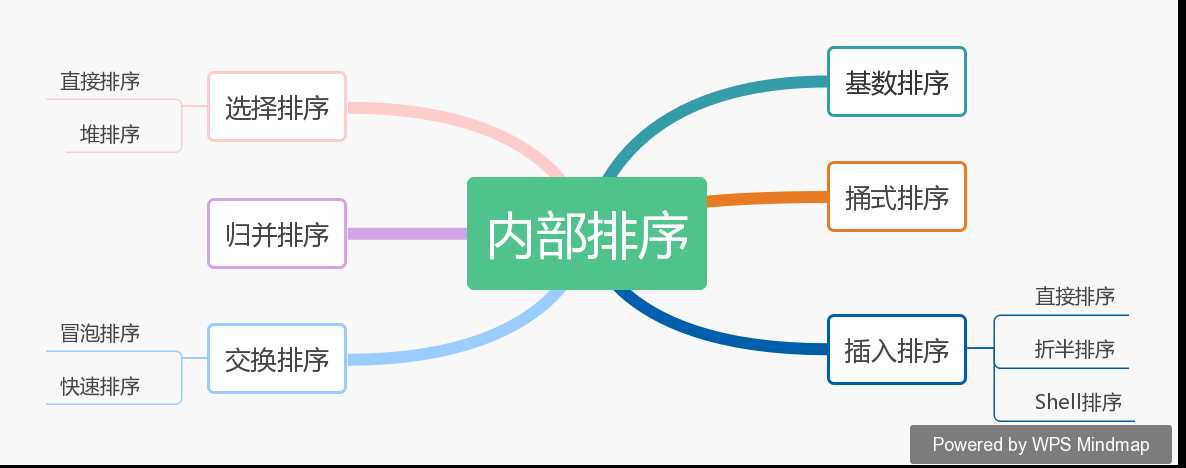
一般我们所说排序指的就是内部排序,常见的内部排序又可以分为6大类。
1 package sort; 2 3 // 定义一个数据包装类 4 class DataWrap implements Comparable<DataWrap> 5 { 6 int data; 7 String flag; 8 public DataWrap(int data, String flag) 9 { 10 this.data = data; 11 this.flag = flag; 12 } 13 public String toString() 14 { 15 return data + flag; 16 } 17 // 根据data实例变量来决定两个DataWrap的大小 18 public int compareTo(DataWrap dw) 19 { 20 return this.data > dw.data ? 1 21 : (this.data == dw.data ? 0 : -1); 22 } 23 }
选择排序方法有两种,直接选择排序和堆排序。直接选择排序简单直观,但是性能较差;堆排序较为高效,但是实现起来较为复杂。
直接选择排序思想:程序遍历n个数,然后比较出最大的一个与最后一个数进行交换,最大值确定好了;接下来遍历n-1,找个这n-1个数中的最大值并且交换位置,直至n=0位置。
该排序方法的数据交换次数是,但是比较次数较多。总的时间效率是。空间效率是,并且算法不稳定。
1 package sort; 2 3 import java.util.*; 4 5 public class SelectSort 6 { 7 public static void selectSort(DataWrap[] data) 8 { 9 System.out.println("开始排序"); 10 int arrayLength = data.length; 11 // 依次进行n-1趟比较, 第i趟比较将第i大的值选出放在i位置上。 12 for (int i = 0; i < arrayLength - 1 ; i++ ) 13 { 14 // minIndex永远保留本趟比较中最小值的索引 15 int minIndex = i ; 16 // 第i个数据只需和它后面的数据比较 17 for (int j = i + 1 ; j < arrayLength ; j++ ) 18 { 19 // 如果第minIndex位置的数据 > j位置的数据 20 if (data[minIndex].compareTo(data[j]) > 0) 21 { 22 // 将j的值赋给minIndex 23 minIndex = j; 24 } 25 } 26 // 每趟比较最多交换一次 27 if (minIndex != i) 28 { 29 DataWrap tmp = data[i]; 30 data[i] = data[minIndex]; 31 data[minIndex] = tmp; 32 } 33 System.out.println(java.util.Arrays.toString(data)); 34 } 35 } 36 public static void main(String[] args) 37 { 38 DataWrap[] data = { 39 new DataWrap(21 , ""), 40 new DataWrap(30 , ""), 41 new DataWrap(49 , ""), 42 new DataWrap(30 , "*"), 43 new DataWrap(16 , ""), 44 new DataWrap(9 , "") 45 }; 46 System.out.println("排序之前:\n" 47 + java.util.Arrays.toString(data)); 48 selectSort(data); 49 System.out.println("排序之后:\n" 50 + java.util.Arrays.toString(data)); 51 } 52 }
堆排序的思路:将数据建立成最大(小)堆,将根节点与最后一个节点交换;重复上面的过程。
1)堆树是一颗完全二叉树;
2)堆树中某个节点的值总是不大于或不小于其孩子节点的值;
3)堆树中每个节点的子树都是堆树。
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。如下图所示,左边为最大堆,右边为最小堆。
引用:https://www.cnblogs.com/zf-blog/p/9010977.html
堆排序是选择算法的改进,可以减少选择排序中的比较次数,进而减少排序时间。对于堆排序来说,有n个数据,需要进行n-1次建堆,每次建堆本身耗时为,所以其时间效率为,堆排序是不稳定的。
1 package sort; 2 3 4 5 public class HeapSort { 6 public static void heapSort(DataWrap[] data) { 7 System.out.println("开始排序"); 8 int arrayLength=data.length; 9 //循环建堆 10 for(int i=0;i<arrayLength-1;i++) { 11 //建堆 12 buildMaxdHeap(data,arrayLength-1-i); 13 //交换堆与最后一个的数据 14 swap(data,0,arrayLength-1-i); 15 System.out.println(java.util.Arrays.toString(data)); 16 } 17 } 18 19 private static void swap(DataWrap[] data, int i, int j) { 20 // TODO Auto-generated method stub 21 DataWrap tmp=data[i]; 22 data[i]=data[j]; 23 data[j]=tmp; 24 25 26 } 27 28 private static void buildMaxdHeap(DataWrap[] data, int lastIndex) { 29 //从lastIndex出节点(最后一个)的父节点开始 30 for(int i=(lastIndex-1)/2;i>+0;i--) { 31 //k保存当前正在判断的点 32 int k=i; 33 //如果当前K节点的子节点存在 34 while(k*2+1<=lastIndex) { 35 //k节点的左子节点的索引 36 int biggerIndex=2*k+1; 37 //判断是否存在右子节点 38 if(biggerIndex<lastIndex) { 39 biggerIndex++; 40 } 41 if((data[k].compareTo(data[biggerIndex])<0)) { 42 swap(data,k,biggerIndex); 43 k=biggerIndex; 44 }else { 45 break; 46 } 47 } 48 } 49 } 50 public static void main(String[] args) 51 { 52 DataWrap[] data = { 53 new DataWrap(21 , ""), 54 new DataWrap(30 , ""), 55 new DataWrap(49 , ""), 56 new DataWrap(30 , "*"), 57 new DataWrap(21 , "*"), 58 new DataWrap(16 , ""), 59 new DataWrap(9 , "") 60 }; 61 System.out.println("排序之前:\n" 62 + java.util.Arrays.toString(data)); 63 heapSort(data); 64 System.out.println("排序之后:\n" 65 + java.util.Arrays.toString(data)); 66 } 67 }
交换排序的主体操作是对数组中的数据不断的进行交换操作。交换排序主要有冒泡排序和快速排序。
冒泡排序思路:类似于鱼吐泡泡,一个接着一个,如果靠近鱼的泡泡比远离鱼的泡泡大,则两个泡泡就会交换。一次执行,就成了一串有序的泡泡。
时间效率:;空间效率:;算法是有序的;
1 package sort; 2 3 public class BubbleSort { 4 public static void bubbleSort(DataWrap[] data) { 5 System.out.println("开始排序"); 6 int arrayLength=data.length; 7 for(int i=0;i<arrayLength-1;i++) { 8 for(int j=0;j<arrayLength-1-i;j++) { 9 if(data[j].compareTo(data[j+1])>0) { 10 DataWrap tmp=data[j+1]; 11 data[j+1]=data[j]; 12 data[j]=tmp; 13 } 14 } 15 System.out.println(java.util.Arrays.toString(data)); 16 } 17 } 18 19 public static void main(String[] args) { 20 DataWrap[] data = { new DataWrap(9, ""), new DataWrap(16, ""), new DataWrap(21, "*"), new DataWrap(23, ""), 21 new DataWrap(30, ""), new DataWrap(49, ""), new DataWrap(21, ""), new DataWrap(30, "*") }; 22 System.out.println("排序之前:\n" + java.util.Arrays.toString(data)); 23 bubbleSort(data); 24 System.out.println("排序之后:\n" + java.util.Arrays.toString(data)); 25 } 26 }
快速排序的思路:如列队一样,先选择一个士兵为基准,比该士兵高则站在其后面,比该士兵矮则站在其前面,这样大致将队伍分为了两个子列。然后在这两个子进行递归。
空间效率:,算法并不稳定。
1 package sort; 2 import java.util.*; 3 4 5 public class QuickSort 6 { 7 // 将指定数组的i和j索引处的元素交换 8 private static void swap(DataWrap[] data, int i, int j) 9 { 10 DataWrap tmp; 11 tmp = data[i]; 12 data[i] = data[j]; 13 data[j] = tmp; 14 } 15 // 对data数组中从start~end索引范围的子序列进行处理 16 // 使之满足所有小于分界值的放在左边,所有大于分界值的放在右边 17 private static void subSort(DataWrap[] data 18 , int start , int end) 19 { 20 // 需要排序 21 if (start < end) 22 { 23 // 以第一个元素作为分界值 24 DataWrap base = data[start]; 25 // i从左边搜索,搜索大于分界值的元素的索引 26 int i = start; 27 // j从右边开始搜索,搜索小于分界值的元素的索引 28 int j = end + 1; 29 while(true) 30 { 31 // 找到大于分界值的元素的索引,或i已经到了end处 32 while(i < end && data[++i].compareTo(base) <= 0); 33 // 找到小于分界值的元素的索引,或j已经到了start处 34 while(j > start && data[--j].compareTo(base) >= 0); 35 if (i < j) 36 { 37 swap(data , i , j); 38 } 39 else 40 { 41 break; 42 } 43 } 44 swap(data , start , j); 45 // 递归左子序列 46 subSort(data , start , j - 1); 47 // 递归右边子序列 48 subSort(data , j + 1, end); 49 } 50 } 51 public static void quickSort(DataWrap[] data) 52 { 53 subSort(data , 0 , data.length - 1); 54 } 55 public static void main(String[] args) 56 { 57 DataWrap[] data = { 58 new DataWrap(9 , ""), 59 new DataWrap(-16 , ""), 60 new DataWrap(21 , "*"), 61 new DataWrap(23 , ""), 62 new DataWrap(-30 , ""), 63 new DataWrap(-49 , ""), 64 new DataWrap(21 , ""), 65 new DataWrap(30 , "*"), 66 new DataWrap(13 , "*") 67 }; 68 System.out.println("排序之前:\n" 69 + java.util.Arrays.toString(data)); 70 quickSort(data); 71 System.out.println("排序之后:\n" 72 + java.util.Arrays.toString(data)); 73 } 74 }
插入排序主要分为直接插入排序、Shell排序和折半排序。
直接插入排序思路:类似于把一堆杂乱的且大小不一的碗按从大到小(从小到大不符合实际)排序。我可以先拿出一个碗,然后在拿出碗与之比较;这两个碗排好序后,再拿出一个碗进行比较,插在其合适的顺序上,以此方式直至最后一个碗位置。
最坏情况的时间复杂度:;空间复杂度:;该算法是稳定的。
1 package sort; 2 3 public class insertSort { 4 public static void insertSort(DataWrap[] data) { 5 System.out.println("开始排序"); 6 int arrayLenght=data.length; 7 for(int i=1;i<arrayLenght;i++) { 8 DataWrap tmp=data[i]; 9 10 if(data[i].compareTo(data[i-1])<0){ 11 int j=i-1; 12 for(;j>=0&&data[j].compareTo(tmp)>0;j--) { 13 data[j+1]=data[j]; 14 } 15 16 data[j+1]=tmp; 17 } 18 System.out.println(java.util.Arrays.toString(data)); 19 } 20 21 } 22 public static void main(String[] args) 23 { 24 DataWrap[] data = { 25 new DataWrap(9 , ""), 26 new DataWrap(-16 , ""), 27 new DataWrap(21 , "*"), 28 new DataWrap(23 , ""), 29 new DataWrap(-30 , ""), 30 new DataWrap(-49 , ""), 31 new DataWrap(21 , ""), 32 new DataWrap(30 , "*"), 33 new DataWrap(13 , "*") 34 }; 35 System.out.println("排序之前:\n" 36 + java.util.Arrays.toString(data)); 37 insertSort(data); 38 System.out.println("排序之后:\n" 39 + java.util.Arrays.toString(data)); 40 } 41 }
思路:与二分法有点相似。因为之前的数据是排好序的,因此为了减少比较次数,可以选择之前数据的中点与要插入的数据进行比较。我们拿到一个碗,把它插在已经排好的碗中时,可以先看中间的碗,如果中间的碗比插入的碗大,在进行二分即可。
算法可能不稳定;
1 package sort; 2 3 public class BinaryInsertSort 4 { 5 public static void binaryInsertSort(DataWrap[] data) 6 { 7 System.out.println("开始排序:\n"); 8 int arrayLength = data.length; 9 for(int i = 1 ; i < arrayLength ; i++) 10 { 11 // 当整体后移时,保证data[i]的值不会丢失 12 DataWrap tmp = data[i]; 13 int low = 0; 14 int high = i - 1; 15 while(low <= high) 16 { 17 // 找出low、high中间的索引 18 int mid = (low + high) / 2; 19 // 如果tmp值大于low、high中间元素的值 20 if(tmp.compareTo(data[mid]) > 0) 21 { 22 // 限制在索引大于mid的那一半中搜索 23 low = mid + 1; 24 } 25 else 26 { 27 // 限制在索引小于mid的那一半中搜索 28 high = mid - 1; 29 } 30 } 31 // 将low到i处的所有元素向后整体移一位 32 for(int j = i ; j > low ; j--) 33 { 34 data[j] = data[j - 1]; 35 } 36 // 最后将tmp的值插入合适位置 37 data[low] = tmp; 38 System.out.println(java.util.Arrays.toString(data)); 39 } 40 } 41 public static void main(String[] args) 42 { 43 DataWrap[] data = { 44 new DataWrap(9 , ""), 45 new DataWrap(-16 , ""), 46 new DataWrap(21 , "*"), 47 new DataWrap(23 , ""), 48 new DataWrap(-30 , ""), 49 new DataWrap(-49 , ""), 50 new DataWrap(21 , ""), 51 new DataWrap(30 , "*"), 52 new DataWrap(30 , "") 53 }; 54 System.out.println("排序之前:\n" 55 + java.util.Arrays.toString(data)); 56 binaryInsertSort(data); 57 System.out.println("排序之后:\n" 58 + java.util.Arrays.toString(data)); 59 } 60 }
Shell排序方法思路:以一个较为合适的步长h,让数据中相差为h的步数进行排序;让后将步长改为h/2,在进行排序;递归下去,直至h=1。(当h=1是,可以认为此时的希尔排序算法就是直接插入排序算法)。对于直接插入算法来说,如果原始数据大部分是有序的,数据的移动操作就会较少。利用希尔排序算法就是把原始数据做到基本有序,有效的减少数据移动的操作。
1 public class ShellSort 2 { 3 public static void shellSort(DataWrap[] data) 4 { 5 System.out.println("开始排序:"); 6 int arrayLength = data.length; 7 // h变量保存可变增量 8 int h = 1; 9 // 按h * 3 + 1得到增量序列的最大值 10 while(h <= arrayLength / 3) 11 { 12 h = h * 3 + 1; 13 } 14 while(h > 0) 15 { 16 System.out.println("===h的值:" + h + "==="); 17 for (int i = h ; i < arrayLength ; i++ ) 18 { 19 // 当整体后移时,保证data[i]的值不会丢失 20 DataWrap tmp = data[i]; 21 // i索引处的值已经比前面所有值都大,表明已经有序,无需插入 22 // (i-1索引之前的数据已经有序的,i-1索引处元素的值就是最大值) 23 if (data[i].compareTo(data[i - h]) < 0) 24 { 25 int j = i - h; 26 // 整体后移h格 27 for ( ; j >= 0 && data[j].compareTo(tmp) > 0 ; j-=h) 28 { 29 data[j + h] = data[j]; 30 } 31 // 最后将tmp的值插入合适位置 32 data[j + h] = tmp; 33 } 34 System.out.println(java.util.Arrays.toString(data)); 35 } 36 h = (h - 1) / 3; 37 } 38 } 39 public static void main(String[] args) 40 { 41 DataWrap[] data = { 42 new DataWrap(9 , ""), 43 new DataWrap(-16 , ""), 44 new DataWrap(21 , "*"), 45 new DataWrap(23 , ""), 46 new DataWrap(-30 , ""), 47 new DataWrap(-49 , ""), 48 new DataWrap(21 , ""), 49 new DataWrap(30 , "*"), 50 new DataWrap(30 , ""), 51 }; 52 System.out.println("排序之前:\n" 53 + java.util.Arrays.toString(data)); 54 shellSort(data); 55 System.out.println("排序之后:\n" 56 + java.util.Arrays.toString(data)); 57 } 58 }
归并排序基本思想:就是将两个有序的序列合成一个新的有序序列。其时间效率为,需要一个与原始序列同样大的辅助序列,因此空间效率较差。算法是稳定的。
1 class DataWrap implements Comparable<DataWrap> 2 { 3 int data; 4 String flag; 5 public DataWrap(int data, String flag) 6 { 7 this.data = data; 8 this.flag = flag; 9 } 10 public String toString() 11 { 12 return data + flag; 13 } 14 // 根据data实例变量来决定两个DataWrap的大小 15 public int compareTo(DataWrap dw) 16 { 17 return this.data > dw.data ? 1 18 : (this.data == dw.data ? 0 : -1); 19 } 20 } 21 public class MergeSort 22 { 23 // 利用归并排序算法对数组data进行排序 24 public static void mergeSort(DataWrap[] data) 25 { 26 // 归并排序 27 sort(data , 0 , data.length - 1); 28 } 29 /** 30 * 将索引从left到right范围的数组元素进行归并排序 31 * @param data 待排序的数组 32 * @param left 待排序的数组的第一个元素索引 33 * @param right 待排序的数组的最后一个元素的索引 34 */ 35 private static void sort(DataWrap[] data 36 , int left, int right) 37 { 38 if (left < right) 39 { 40 // 找出中间索引 41 int center = (left + right) / 2; 42 // 对左边数组进行递归 43 sort(data, left, center); 44 // 对右边数组进行递归 45 sort(data, center + 1, right); 46 // 合并 47 merge(data, left, center, right); 48 } 49 } 50 /** 51 * 将两个数组进行归并,归并前两个数组已经有序,归并后依然有序。 52 * @param data 数组对象 53 * @param left 左数组的第一个元素的索引 54 * @param center 左数组的最后一个元素的索引,center+1是右数组第一个元素的索引 55 * @param right 右数组的最后一个元素的索引 56 */ 57 private static void merge(DataWrap[] data 58 , int left, int center, int right) 59 { 60 // 定义一个与待排序序列长度相同的临时数组 61 DataWrap[] tmpArr = new DataWrap[data.length]; 62 int mid = center + 1; 63 // third记录中间数组的索引 64 int third = left; 65 int tmp = left; 66 while (left <= center && mid <= right) 67 { 68 // 从两个数组中取出小的放入中间数组 69 if (data[left].compareTo(data[mid]) <= 0) 70 { 71 tmpArr[third++] = data[left++]; 72 } 73 else 74 { 75 tmpArr[third++] = data[mid++]; 76 } 77 } 78 // 剩余部分依次放入中间数组 79 while (mid <= right) 80 { 81 tmpArr[third++] = data[mid++]; 82 } 83 while (left <= center) 84 { 85 tmpArr[third++] = data[left++]; 86 } 87 // 将中间数组中的内容复制拷回原数组 88 // (原left~right范围的内容复制回原数组) 89 while (tmp <= right) 90 { 91 data[tmp] = tmpArr[tmp++]; 92 } 93 } 94 public static void main(String[] args) 95 { 96 DataWrap[] data = { 97 new DataWrap(9 , ""), 98 new DataWrap(-16 , ""), 99 new DataWrap(21 , "*"), 100 new DataWrap(23 , ""), 101 new DataWrap(-30 , ""), 102 new DataWrap(-49 , ""), 103 new DataWrap(21 , ""), 104 new DataWrap(30 , "*"), 105 new DataWrap(30 , "") 106 }; 107 System.out.println("排序之前:\n" 108 + java.util.Arrays.toString(data)); 109 mergeSort(data); 110 System.out.println("排序之后:\n" 111 + java.util.Arrays.toString(data)); 112 } 113 }
原文:https://www.cnblogs.com/tianliang94/p/10458888.html