1 int cal(int n) { 2 int sum = 0; 3 int i = 1; 4 for (; i <= n; ++i) { 5 sum = sum + i; 6 } 7 return sum; 8 }
1 int cal(int n) { 2 int sum = 0; 3 int i = 1; 4 int j = 1; 5 for (; i <= n; ++i) { 6 j = 1; 7 for (; j <= n; ++j) { 8 sum = sum + i * j; 9 } 10 } 11 } 12
1 i=1; 2 while (i <= n) { 3 i = i * 2; 4 }
1 void print(int n) { 2 int i = 0; 3 int[] a = new int[n]; 4 for (i; i <n; ++i) { 5 a[i] = i * i; 6 } 7 8 for (i = n-1; i >= 0; --i) { 9 print out a[i] 10 } 11 }
1 void print(int n) { 2 int i = 0; 3 int[] a = new int[n]; 4 for (i; i <n; ++i) { 5 a[i] = i * i; 6 } 7 8 for (i = n-1; i >= 0; --i) { 9 print out a[i] 10 } 11 }
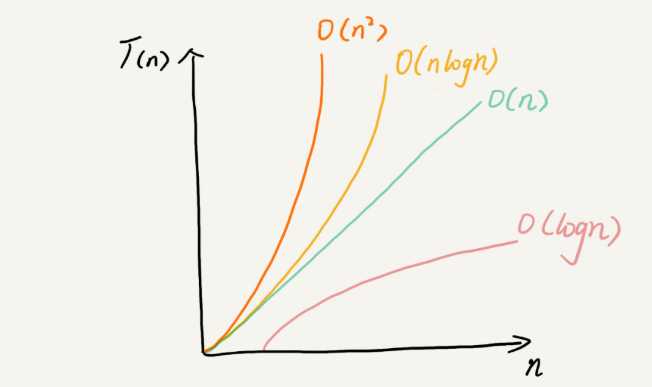
O(n)
原文:https://www.cnblogs.com/huangguoming/p/10458912.html