Constructing Chimney（HDU-4332）

题目描述：

Now we are planning to construct a big chimney. The chimney’s section is a 3×3 square and the center of it will have nothing like the picture below. Now we only have a lot of bricks whose size if 1×1×2, and we want to build a chimney whose height is N, so can help us to calculate how many ways we can build the chimney? The answer may be very large, so you can just tell the answer‘s remainder divided by 1000000007.

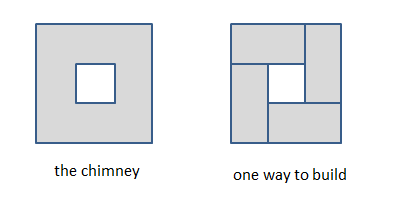
用1×1×2的砖头摆出如图所示的烟囱，可以横着摆也可以竖着摆，求摆出n层高的烟囱会有多少种不同的方案。

思路：

这题其实最难想的就是dp转移，变态的细节非常的多。

首先要考虑的就是状态定义，若是一层一层的进行转移我们都考虑他们所在当前层的状态，我们用一个8位二进制数来表示当前层的状态，当然，1表示砖，0表示没有砖。

若是暴力转移我们便有：
$dp[i][stat]=dp[i-1][stat2]*met[stat][stat2]$

注意$met[stat][stat2]$表示状态由当前层的stat2到下一层的stat的方案数

若是直接这样转移，复杂度绝对爆炸，所以就考虑用矩阵乘法快速幂来进行操作。

不过在开始定义矩阵时，先想一想：就算使用矩阵优化，复杂度也是$O(256^3*log(n))$,还是很可能会超时（不过卡常卡的好话或许也可以吧。。个人没试过）。那么咋们看一下这$256$个状态（毕竟那个log也没什么好优化的），应该比较好想到所有$1$的个数为奇数个的状态都是无效的，因为这样就无法把当前层填满而又不会填到下一层了。这样复杂度就够了，不过好像可以再把所有旋转相同的状态也去掉，使得最后只有七十多种状态，不过旋转判定有点复杂，我就懒得想了。。。

最后就是预处理最初矩阵，其实就是把所有能够相互转移的状态找出，注意是当前层的状态转移到下一层的状态，所以$0$和$1$是哪一层的$0$和$1$分清楚，别的也没什么了，判是否可行的方法有很多，就不在过多赘述了。

代码

#include<bits/stdc++.h>
#define FOR(i,l,r) for(int i=l,END=r;i<=END;i++)
#define DOR(i,r,l) for(int i=r,END=l;i>=END;i--)
#define loop(i,n) for(int i=0,END=n;i<END;i++)
#define mms(a,x) memset(a,x,sizeof a)
#define sf scanf
#define pf printf
#define lowbit(x) ((x)&(-x))
using namespace std;
const int P=1e9+7,N=(1<<8),M=N>>1;
int n;
bool flag[N];
struct Matrix{//矩阵 
    int num[N][N];
    void clear(){mms(num,0);}
    void init(){clear();loop(i,M)num[i][i]=1;}
    void Print(){loop(i,M)loop(j,M)pf("%d%c",num[i][j],j==M-1?'\n':' ');}
    Matrix operator*(const Matrix &A)const{
        Matrix ans;
        ans.clear();
        loop(i,M)loop(j,M)
            loop(k,M)ans.num[i][j]=(ans.num[i][j]+1ll*num[i][k]*A.num[k][j])%P;
        return ans;
    }
}Pow[35];
bool is1(int x,int pos){return (x>>pos)&1;}
bool check(int x,int y){//判定是否可行 
    int mark=2;
    loop(i,8){
        if(is1(x,i)&&is1(y,i)){//若在上一层已有，那么只能横着放砖块，所以它的下一位也要是1 
            if(i<7&&is1(x,i+1)&&is1(y,i+1))i++;
            else {mark--;break;};   
        }
        else if(!is1(x,i)&&!is1(y,i)){mark--;break;};
    }
    x|=(x&1)<<8;
    y|=(y&1)<<8;
    //把第一位移到最后面
    DOR(i,8,1){//到这再来一次，这次能够使第一个和最后一个也考虑到 
        if(is1(x,i)&&is1(y,i)){//同上
            if(i>1&&is1(x,i-1)&&is1(y,i-1))i--;
            else {mark--;break;};
        }
        else if(!is1(x,i)&&!is1(y,i)){mark--;break;};       
    }
    return mark>0;
}
void init(){
    loop(i,N){
        int t=i,cnt=0;
        for(;t;t^=lowbit(t))cnt^=1;
        if(!cnt)flag[i]=1;
    }
    int bx=0,by=0;
    loop(i,N){//预处理矩阵 
        if(flag[i]){
            by=0;
            loop(j,N)if(flag[j])
                Pow[0].num[bx][by++]=check(i,j);
            bx++;
        }
    }
    Pow[0].num[M-1][M-1]++;
    FOR(i,1,32)Pow[i]=Pow[i-1]*Pow[i-1];//预处理快速幂矩阵 
}
int qpow(int n){
    Matrix res;
    res.init();
    loop(i,32)if(is1(n,i))res=res*Pow[i];
    return res.num[M-1][M-1];
}
int main(){
    init();
    int T,kase=0;
    sf("%d",&T);
    while(T--){
        sf("%d",&n);
        pf("Case %d: %d\n",++kase,qpow(n));
    }
    return 0;
}

Constructing Chimney（HDU-4332）

原文：https://www.cnblogs.com/Heinz/p/10459055.html