来自:https://blog.csdn.net/sd9110110/article/details/53558821
一、什么是正规方程
梯度下降法计算参数最优解,过程是对代价函数的每个参数求偏导,通过迭代算法一步步更新,直到收敛到全局最小值,从而得到最优参数。
正规方程是一次性求得最优解。
思想:对于一个简单函数,对参数求导,将其值置为0,就得到参数的值。像下面这样:
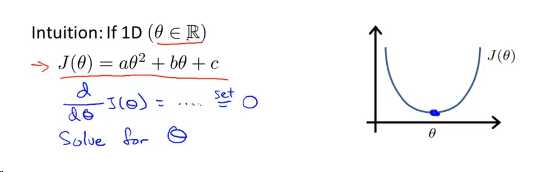
现实例子有很多参数,我们要对这些参数都求偏导数,得到各个参数的最优解,也就是全局最优解。但是困难在于,这样做非常浪费时间。
二、正规方程的使用
举例如下:
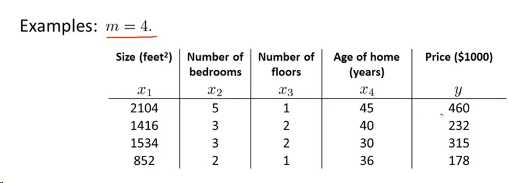
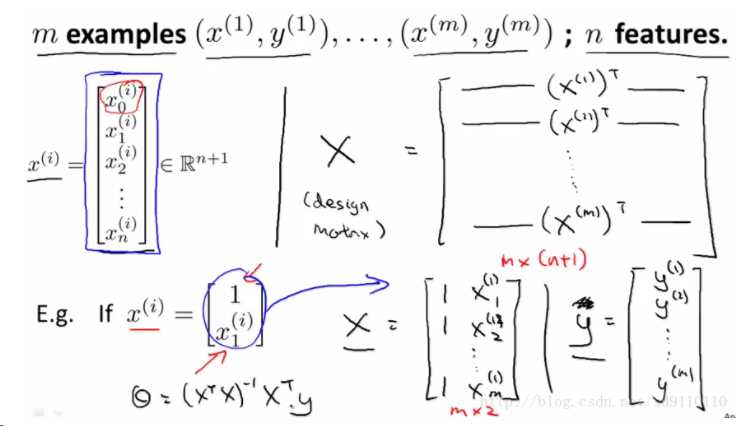
这里4个样本,以及4个特征变量x1,x2,x3,x4,观测结果是y,在列代价函数的时候,需要加上一个末尾参数x0,如下:
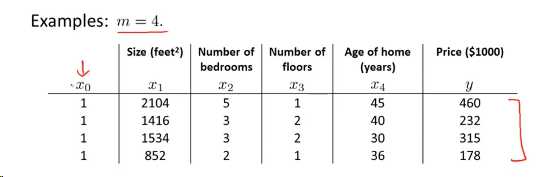
再将特征参数保存在X矩阵中,对观测结果做同样的操作并保存在向量y中,如图:
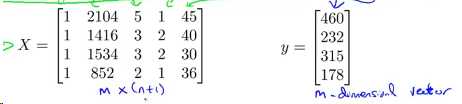
然后我们通过下面这个公式得出参数θ最优解。
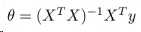
关于这个式子推到:
原文:https://www.cnblogs.com/keye/p/10466300.html