嗯,在学新的数据结构前,先了解一下这个东西有什么用。多字警告。
线段树,顾名思义就是线段构成的树, NOIP知识点中需要掌握的为数不多的数据结构之一,也是NOIP阶段比较常见的数据结构,就是线段树,即使是NOI也经常见到线段树的影子,算是比较常用的数据结构了。
线段树的作用很多,最基本的是$O(logn)$地维护与查询区间的一些信息(都是符合结合律的一些操作),比如区间最值,区间和/积等等,而随着对线段树的理解更深,可能接触到更多题目,用线段树维护一些奇奇怪怪的东西。当然,这篇文章讲普通线段树,只能维护一些静态的问题,不是不支持修改,而是不能支持对历史版本的修改。
举个栗子,用线段树能维护一个序列的区间和,支持询问、区间/单点修改,但是,若说“每次操作得到一个历史序列,之后的操作可能对不同历史序列进行操作,再得到新的序列,还要询问某个历史的序列信息”,即需要“持久化”,这样普通线段树就无能为力了。如果对每个操作建个线段树,空间时间都受不了,以后会遇到主席树(也叫持久化线段树)能解决这个问题,不过是NOI的东西了,这篇文章暂不讨论。
有个本来想写成“后记”的,想了想还是放在了前面。可以先看完下面再回来看这个。还有个叫做zkw线段树的东西,是普通线段树的递推式写法,我们平时用线段树几乎都是递归写法。但是递归要调用系统栈,分配资源,空间时间消耗(指常数方面)肯定要大些。于是就有了递推式的zkw线段树,在区间加的模板题中常数小了差不多一倍。但作为代价,zkw线段树不支持高级操作,连同时区间加+区间乘都不行,灵活性比普通线段树低很多(反正我是不喜欢)。
给个定心针,线段树真的很简单,比什么什么平衡树(虽说与线段树毫无联系)不知道简单多少,代码实现也很容易,是那种就算不理解,打几遍板子也就能记住的数据结构。
1、引入问题
那么先从模板开始,引入一个小问题(洛咕传送门)。
把题目放这。先来张图,看看我们要建个什么东西。
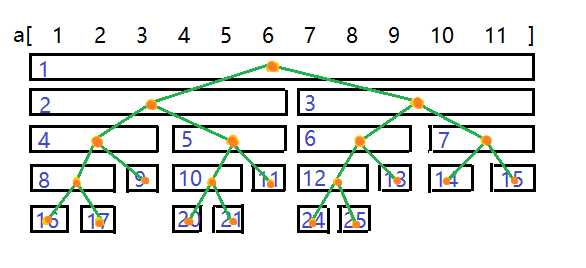
图中把方块全部换成节点(也就是我们需要记录、维护信息的节点),就能得到一颗二叉树,叶节点对应了我们要维护的序列单个元素,其他节点对应了不同大小的区间,由子节点,也就是子区间合并而来。
蓝色的数字是节点编号......那为什么$18、19、22、23$号节点不见了?为什么编号不按顺序来呢?首先排除编号被我吃掉了。可以注意到,对于节点i左孩子编号为$i\times2$, 右孩子编号为$i\times2+1$。这个性质很重要,另外,如果根节点从1开始标号,可以保证左孩子节点编号为偶数,右孩子为奇数,这样可以用$i<<1$、$(i<<1)|1$表示左右孩子编号了($i<<1$相当于$i\times2$,而$"|1"$的操作用到了奇偶的性质,二进制运算了解一下)。
现在我在讲数组版的线段树,当然还有指针版(数组指针)、真·指针版,但是普通线段树最常用的还是数组版,也就是我要说的写法。(另外,前面几个都是递归写法,还有递推写法,待会儿再说咕咕咕)
先看看我们需要建立哪些变量:
#define lc(x) (x<<1)
#define rc(x) ((x<<1)|1)
struct SegNode {
ll sum, addtag;
// @sum: 当前节点维护的区间和
// @addtag: lazy标记,记录当前节点表示的区间每个元素增加了多少
} node[M];昂,就这些,$node$是线段树的节点,我比较喜欢写成结构体,另外注意到两个$#define$定义,$lc(x)、rc(x)$就是$x$的左右孩子节点编号,用位运算是会减小常数的。
关于线段树的大小$M$,通常是开成序列长度的$4$倍。
2、build()
接下来就是考虑怎么建造了。
二叉树的构造, 当然是选择$dfs$啦。我们需要像分治一样, 每次把区间拆成两部分,向下递归建造,直到遇到叶节点,记录下信息(对应原序列中单个元素),再递归回去的过程中维护靠上面节点的信息,也就是合并子区间信息。
下面是建造函数$build()$的代码,里面有详细的注释:
void build(int l = 1, int r = n, int k = 1) {
// l, r表示当前递归处理到序列的区间[l, r]
// k表示当前所在的线段树节点编号
// 大多情况下l=1, r=n, k=1开始, 所以这里用了缺省函数, 但注意这个n变量(即原序列长度)要设成全局变量
if (l == r) {
node[k].sum = a[l];
// 对应到一个元素, 则直接把这个节点(就是叶节点)sum值设置为这个元素, 并结束递归
} else {
int mid = (r+l)>>1; // 等效于(l+2)/2 // 把区间拆成[l, mid], [mid+1, r]
build(l, mid, lc(x)); // 向左递归
build(mid+1, r, rc(x)); // 向右递归
update(k); // 下面的子树构造完毕, 递归回去, 维护信息
}
}3、intervalAdd()
然后是修改操作,这里是区间加操作,首先是要找到需要修改的区间,在对应节点上进行修改就行了,递归过程很像$build()$,只是需要加以判断来找到目标节点/区间。
光说很难理解,那就给张图,再之前的那张图上,我们建了一个线段树,现在,我们需要给原序列区间[5, 9]加上一个值,我就用红色的框圈出我们实际要改变的节点:
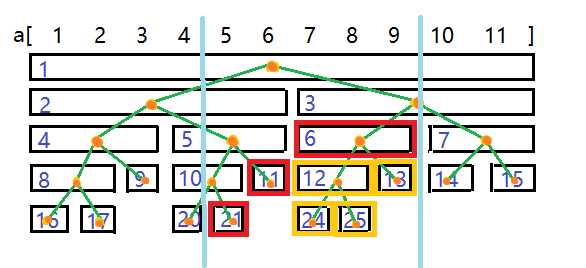
蓝色的线画出了区间[5, 9]对应的节点(只有完全在线内才是[5, 9]的子区间),我们需要修改[5, 9]子区间对应的节点,并且一次修改最少的节点(子区间),不重复地覆盖这个区间,前面说了,红色的节点就是是一次modify修改操作需要修改的节点,但黄色的点也是需要维护的,可为什么不一次修改完呢?
首先,一次修改完会让时间复杂度增加很多,而且,这个修改可以先放那,用lazy标记$addtag$记录一下,等需要用到这些黄色节点的时候再更新她们。完全不知道lazy标记是什么?后面和$pushdown()$函数、$update()$函数一起讲,可以先按顺序看完,看完后面再回来看一遍,读者一定会有所体会的。
放代码:
void add(int L, int R, ll v, int l = 1, int r = n, int k = 1) {
// @L, R, v: 当前操作要将序列的的区间[L, R]每个元素加上一个值v
// @l, r, k: 同前面的build()的l, r, k, 表示当前处理到线段树的节点node[k],表示区间[l, r]
if (L <= l && r <= R) {
// 一旦找到子区间(就是红色的点)就更新, 并结束递归
// 因为是从上到下递归的, 可以保证这个子区间尽可能大
// 而且因为下面的[l, mid], [mid+1, r]是连续的, 这样就保证了一定可以把目标区间不重不漏地覆盖起来
node[k].sum += (r-l+1LL) * v;
node[k].addtag += v;
} else {
int mid = (l+r)>>1; // mid = (l+r)/2
pushdown(k, mid-l+1, r-mid); // 在用(遍历)到下面的节点时,先把lazy标记推下去,即先保证下面的节点维护的是正确的信息
if (L <= mid) add(L, R, v, l, mid, lc(k)); // 如果左边的区间还包含的目标区间(或一部分), 就向左递归
if (mid < R) add(L, R, v, mid+1, r, rc(k)); // 同理, 向右递归
update(k);
// 子节点只要改变, 父节点就要重新更新信息
}
}4、queryIntervalSum()
现在就要考虑询问操作了,询问一段区间的和,和$add()$真滴像,只是加了return、没有改变信息而已。
再放张图辅助理解,假设我们要访问[5, 9]这个区间...红色的点是我们访问到的最后的节点,把这些节点信息合并起来就是ans:
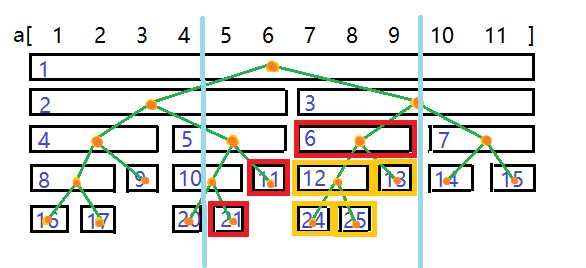
我真的没有偷懒。原理相同,直接放代码:
ll query(int L, int R, int l = 1, int r = n, int k = 1) {
// @L, R: 当前操作要询问区间[L, R]的区间和
// @l, r, k: Ctrl+C, Ctrl+V(add()里l,r,k的定义)
if (L <= l && r <= R) {
return node[k].sum;
// 找到红色的节点, 直接返回她的信息
// 和add()原理一样,可以保证不重不漏覆盖目标区间
} else {
int mid = (l+r)>>1; // rua————
ll ret = 0;
pushdown(k, mid-l+1, r-mid);
// 在询问(使用)到某个节点前先维护好她之前的信息, 就是把lazy标记pushdown下去
if (L <= mid) ret += query(L, R, l, mid, lc(k)); // 如果左边还包含目标区间或其一部分, 向左递归, 把左边那部分区间的信息合并上来
if (mid < R) ret += query(L, R, mid+1, r, rc(k)); // 同理向右递归
return ret;
// 返回合并后的信息
// 这里不需要update, 因为没有节点被改变
}
}5、update()与pushdown()
不要方,我没有忘记重要的东西。
前面突然出现的$update()$和$pushdown()$函数,这两个函数,怎么说呢,我觉得是线段树的灵魂,尤其是前者,线段树的灵活性就在于$update()$函数,还有就是关于lazy标记和下传标记的函数。
$update(k)$的作用是把线段树节点k的子节点的信息合并到k上。一旦某个节点子节点信息改变,就要update一下这个节点。
对于这题,我们只需要维护节点代表的区间和就行了,于是$update()$随便写写就行了:
void update(int now) {
// @now: 需要update的线段树节点编号
node[now].sum = node[lc(now)].sum + node[rc(now)].sum;
// 区间和等于子区间和
// 我的注释真_详细, 真_感动
}然而有的题目是需要维护很多奇怪的信息,比如区间最大前后缀和、区间最大子区间和等等,厉害一点的,我见过用来维护一个点数不超过100的图的最小生成树。这就需要做题积累了。
然后就是lazy标记($pushdown()$是用来下传lazy标记的),想想每次modify序列(前文提到的$add()$操作),都O(logn)地从根维护到叶子,即每次到(l == r)时才结束递归,效率并不是很高,但是有个优化的方法,就是tag标记。
这个lazy标记, 前文中是关于区间加的tag——addtag,表示当前区间每个元素已经加上了addtag的值,在访问到这个节点的之前,必须把这个值加上,这样这个节点维护的信息才是最实时的信息,这也就是为什么每次要在访问到子节点前,也就是递归到子节点前pushdow。
当初因为这个纠结了我很长时间的,这题是只有区间加操作,只要下传lazy标记$addtag$,$pushdown()$可以这么写:
void pushdown(int now, int ln, int rn) {
// @now: 从线段树节点now的地方把lazy标记pushdown下去
// @ln, rn: 左右子节点代表的区间的元素数量
if (!node[now].addtag) return;
// 并没有需要pushdown的tag, 那就不pushdown了
SegNode &p = node[now], &pl = node[lc(now)], &pr = node[rc(now)];
// 这么写的话一定要记得加上"&"啊, 我被坑几van次了
pl.sum += p.addtag * ln; pl.addtag += p.addtag;
// 区间每个元素加上值v, 则区间和加上v*区间元素个数
// 记得把addtag也要传下去
pr.sum += p.addtag * rn; pr.addtag += p.addtag;
// 同理
p.addtag = 0;
// 最后别忘了把传过的tag清空
}但是,如果有更多tag呢?比如区间加、区间乘、区间赋值一起出现了呢?我们必须考虑先后顺序,否则一个tag下传可能会影响其他tag以及下面的信息。
我们首先需要明确的是tag的定义:当前区间经历的操作,要传给下面的两个子区间。也就是下传tag的时候,这个区间是已经被修改过的了。然后就是优先度问题,就像加减乘除赋值的运算优先级顺序一样,我们需要把优先级高的先下传,同时优先级高的会影响优先级低的的操作,也就是优先级低的tag也要和信息一起被修改。有点难以名状。后面会有例题详细介绍,这里直接给出常见的几个对数列的操作的tag优先级:赋值settag $\gt$ 区间乘multag $\gt$ 区间加addtag。
6、没了,那就把全部代码放上来吧
前面的代码注释太多了好难看。
啊,这里我把线段树的函数封装到struct里了,struct是好文明,唔呣唔呣。
#include <cstdio>
#include <cstring>
#include <algorithm>
using std::swap;
typedef long long ll;
const int N = 1e6+5;
const int M = 4e6+5;
const int inf = 1e9+7;
#define reset(x, y) memset(x, y, sizeof(x))
#define clean(x) reset(x, 0)
#define qwq register
#define OvO inline
const int MAXIN = 1e5;
char IN[MAXIN],*SS=IN,*TT=IN;
#define getchar() (SS == TT&&(TT = (SS=IN) + fread(IN,1,MAXIN,stdin), SS==TT) ? EOF:*SS++)
template <typename T> OvO T max(T a, T b) { return a > b ? a : b; }
template <typename T> OvO T min(T a, T b) { return a < b ? a : b; }
template <typename T> OvO void read(T &x) {
x = 0; T f = 1; char c = getchar();
while (c<'0' || c>'9') { if (c=='-') f=-1; c = getchar(); }
while (c>='0' && c<='9') { x = x*10+c-'0'; c = getchar(); }
x *= f;
}
// 以上都是板子, 可以当头文件看...
// 不用太在意, 下面只用到了快读read()
// scanf什么的完全可以嘛
bool mark1;
int n, m;
ll a[N];
struct SegNode {
ll sum, addtag;
SegNode(ll sum = 0, ll addtag = 0) :
sum(sum), addtag(addtag){ }
} node[M];
#define lc(x) (x<<1)
#define rc(x) ((x<<1)|1)
struct SegTree {
void update(int now) {
node[now].sum = node[lc(now)].sum + node[rc(now)].sum;
}
void pushdown(int now, int ln, int rn) {
if (!node[now].addtag) return;
SegNode &p = node[now], &pl = node[lc(now)], &pr = node[rc(now)];
pl.sum += p.addtag * ln; pl.addtag += p.addtag;
pr.sum += p.addtag * rn; pr.addtag += p.addtag;
p.addtag = 0;
}
void build(int l = 1, int r = n, int k = 1) {
if (l == r) {
node[k].sum = a[l];
} else {
int mid = (l+r)>>1;
build(l, mid, lc(k));
build(mid+1, r, rc(k));
update(k);
}
}
void add(int L, int R, ll v, int l = 1, int r = n, int k = 1) {
if (L <= l && r <= R) {
node[k].sum += (r-l+1LL) * v;
node[k].addtag += v;
} else {
int mid = (l+r)>>1;
pushdown(k, mid-l+1, r-mid);
if (L <= mid) add(L, R, v, l, mid, lc(k));
if (mid < R) add(L, R, v, mid+1, r, rc(k));
update(k);
}
}
ll query(int L, int R, int l = 1, int r = n, int k = 1) {
if (L <= l && r <= R) {
return node[k].sum;
} else {
int mid = (l+r)>>1;
ll ret = 0;
pushdown(k, mid-l+1, r-mid);
if (L <= mid) ret += query(L, R, l, mid, lc(k));
if (mid < R) ret += query(L, R, mid+1, r, rc(k));
return ret;
}
}
} seg;
bool mark2;
int main()
{
//freopen("testin.txt", "r", stdin);
//freopen("stdout.txt", "w", stdout);
//freopen("testout.txt", "w", stdout);
//printf("Memory:%lfMB\n", (&mark2-&mark1)/1000.0/1000.0); // calc Memory used
read(n); read(m);
for (int i = 1; i <= n; ++i) read(a[i]);
seg.build();
int opt = 0, l = 0, r = 0; ll v = 0;
for (int i = 1; i <= m; ++i) {
read(opt);
if (opt == 1) {
read(l); read(r); read(v);
seg.add(l, r, v);
} else {
read(l); read(r);
printf("%lld\n", seg.query(l, r));
}
}
return 0;
}P3372_[模板]线段树_1 传送门 [上面的模板]
P3870_[TJOI2009]开关 传送门+我写的题解 [上面的模板+小小的转化]
P3373_[模板]线段树_2 传送门 [区间加&区间乘]
P2061_[USACO07OPEN]City_Horizon 传送门+我写的题解 [离散化+区间乘]
还有个同时包含区间和、区间加、区间乘的板子,没找到对应的题目,可以自己打个板子。那么我直接给个综合的板子,这个打通了,上面的两个小模板题也就不算什么了。线段树板子[add & mul & set]。
P1471_方差 传送门+我写的题解 [简单的转化+简单的模板]
P1856_[USACO5.5]Picture 传送门+我写的题解 [扫描线]
原文:https://www.cnblogs.com/IrisEuclase/p/10486890.html