https://vjudge.net/problem/UVA-1607
输入一个由与非门组成的电路,所有输入均相同。为了节约成本,需要将输入接口减少至最少,多出来的输入接口连接常数信号。
与非门真值表如下
| 输入A | 输入B | 输出 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
输入输出细节见原题。
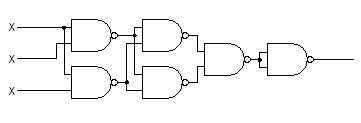
整个电路只有2种输入,那么输出可能有4种,即整个电路的功能可能有4种情况。
| 输入 | 全1 | 全0 |
| 电路1输出 | 1 | 1 |
| 电路2输出 | 1 | 0 |
| 电路3输出 | 0 | 1 |
| 电路4输出 | 0 | 0 |
先输入1和0,测试下,可以快速得到是否为1、4电路
考虑剩下的2、3电路……
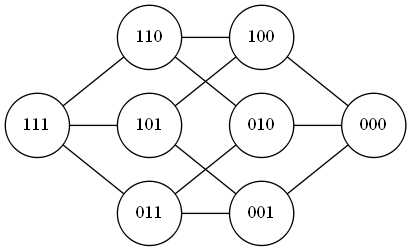
可能是枚举吧= =找到两个结果不同的相邻节点,把不同的位设为x就好了(可是顺序还是要对应……)
时间复杂度$\Omega(m\times 2^n)$——一定TLE,而且枚举的顺序也很怪,可能要枚举多次……就这个例子,能否一笔画完这张图呢……显然是不行的(度数为奇数的点超过了2个)
我们只选000到111种的某一条路线,画成下面的统计图……
设输入x的输出为f(x)
这条路线中就有x10、1x0、10x两种,但必须方向问题……(由0变为1时由 $f(全0)$ 变为 $f(全1)$)
(根据答案编过程)我们可以按照前面全是0后面全是1的路线
如000->100->110->111
那么因为全0和全1的输出不一样,那么这中间一定会出现一次由 $f(全0)$ 到 $f(全1)$ 的变化,而且方向是正确的,因此x最少出现1次。
我们只需要找出这样一种变化即可
可以用“二分法”,但是这种“二分法”找出来的不一定是第一个这种变化
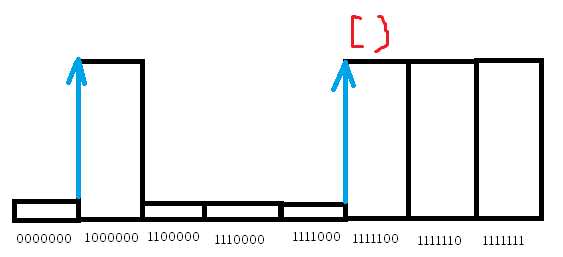
如这种电路最后找出来的就不是第一种这个变化。反正只需要任意一种答案,能找到就可以了。
注意输入的时候的下标从1开始……评测排队一小时后告诉我WA了:(
时间复杂度$O(m\log n)$
AC代码
#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
#include<bits/stdc++.h>
using namespace std;
#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define REPE(r,x,y) for(register int r=(x); r<=(y); r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...)
#endif
#define MAXM 200007
typedef long long LL;
template <class T>
inline void read(T& x) {
char c=getchar();
int f=1;
x=0;
while(!isdigit(c)&&c!=‘-‘)c=getchar();
if(c==‘-‘)f=-1,c=getchar();
while(isdigit(c)) {
x=x*10+c-‘0‘;
c=getchar();
}
x*=f;
}
template <class T>
void write(T x) {
if(x<0) {
putchar(‘-‘);
write(-x);
return;
}
if(x>9) write(x/10);
putchar(x%10+‘0‘);
}
struct circuit {
int id1, id2;
int o;
} cs[MAXM];
int n,m;
//1111000
inline int getout(int k) {
REPE(i,1,m) {
int in1, in2;
in1 = cs[i].id1<0 ? -cs[i].id1<=k : cs[cs[i].id1].o;
in2 = cs[i].id2<0 ? -cs[i].id2<=k : cs[cs[i].id2].o;
cs[i].o = !(in1&&in2);
}
return cs[m].o;
}
int main() {
#ifdef sahdsg
freopen("in.txt", "r", stdin);
#endif
int d;
read(d);
while(0<d--) {
read(n); read(m);
REPE(i,1,m) {
read(cs[i].id1);
read(cs[i].id2);
}
int o0=getout(0);
int on=getout(n);
if(o0==on) {REP(i,0,n) putchar(‘0‘); putchar(‘\n‘); continue;}
int l=0,r=n;
while(l<r) {
int mid = l + (r-l)/2;
int k=getout(mid);
if(k==o0) {
l=mid+1;
} else r=mid;
}
REP(i,0,l-1) putchar(‘1‘);
putchar(‘x‘);
REP(i,l,n) putchar(‘0‘);
putchar(‘\n‘);
}
return 0;
}
原文:https://www.cnblogs.com/sahdsg/p/10493396.html