<题目链接>
题目大意:
有两个人和一个$n*m$的网格,每个格子内有一定数值,一个人A要求从$(1,1)$走到$(n,n)$(只能向右或向下),另一个人B要求从$(n,1)$走到$(1,n)$(只能向右或向上)。相遇时的格子的数值不算(只能相遇一个格子),问你两个人当都到达要求时的地点,最大数值为多少?
解题分析:
先得到从四个角出发到网格内每个点的最大值,然后再枚举交点,更新最大值。为什么要考虑从四个角出发呢?因为枚举交点的时候,两条路线会断成四个部分,这四个部分均取最大值,就能得到两条路线总和的最大值。对于每个交点来说,路线有两种情况。
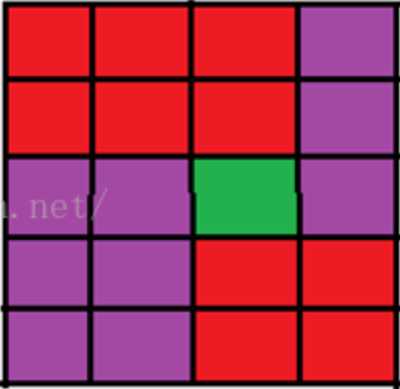
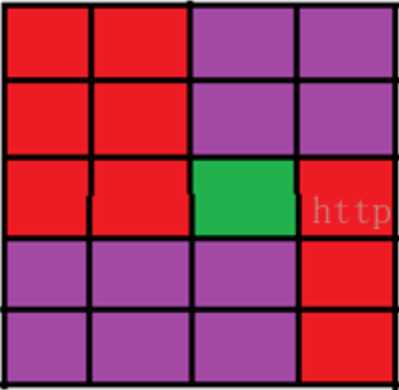
(图一) (图二)
#include <bits/stdc++.h> using namespace std; #define rep(i,s,t) for(int i=s;i<=t;i++) #define srep(i,s,t) for(int i=s;i>=t;i--) const int N = 1e3+5; int n,m,mpa[N][N]; int dp1[N][N],dp2[N][N],dp3[N][N],dp4[N][N]; int solve(){ int ans=0; rep(i,2,n-1) rep(j,2,m-1){ //枚举交点,因为只能有一个交点,所以该交点不可能在边界上 int tmp1=dp1[i-1][j]+dp2[i+1][j]+dp3[i][j-1]+dp4[i][j+1]; //交点的两种可能路径情况 int tmp2=dp1[i][j-1]+dp2[i][j+1]+dp3[i+1][j]+dp4[i-1][j]; ans=max(ans,max(tmp1,tmp2)); }return ans; } int main(){ scanf("%d%d",&n,&m); rep(i,1,n) rep(j,1,m) scanf("%d",&mpa[i][j]); rep(i,1,n) rep(j,1,m) dp1[i][j]=max(dp1[i-1][j],dp1[i][j-1])+mpa[i][j]; //左上角出发到全局的最大值 srep(i,n,1) srep(j,m,1) dp2[i][j]=max(dp2[i+1][j],dp2[i][j+1])+mpa[i][j]; //右下角出发 srep(i,n,1) rep(j,1,m) dp3[i][j]=max(dp3[i+1][j],dp3[i][j-1])+mpa[i][j]; //左下角出发 rep(i,1,n) srep(j,m,1) dp4[i][j]=max(dp4[i-1][j],dp4[i][j+1])+mpa[i][j]; //右上角出发 //之所以要分成四个部分,就是因为对交点的考虑,会将一条路线分成两部分 int ans=solve(); printf("%d\n",ans); }
Codeforces 429B Working out (线性DP)
原文:https://www.cnblogs.com/00isok/p/10505233.html