机器学习的几大类:
1.推荐
2.分类
3.聚类
4.回归
5.用户画像
6.深度学习
7.人工神经网络
8.关联分析
分类算法:
1.朴素贝叶斯
2.决策树
3.随机森林
4.支持向量机(SVM)
5.隐马尔可夫模型
6.遗传算法
分类属于有监督的学习过程,可以根据经验或者数学推导等辅助的方法给机器一些指导,帮助机器去噪,收敛,剪枝。让计算更加快捷和准确。
分类问题:
1.二值分类:1或0----->是或否
2.多值分类
分类必须有两样东西:
1.标签(label)
2.训练数据
有label的算法------>监督学习 ------>分类,回归
监督的是什么? label
数据(大量)---->模型----->预测
无label的算法------>无监督学习------>聚类
------------------------------------------------------------------------------
分类
定义:给定一个对象X,将其划分到预定义好的某一个类别Yi中
– 输入:X
– 输出:Y(取值于有限集合{y1,y2,……,yn})
二值分类例子:
假设:给一篇文章,判断是军事还是财经
输入的就是文章,输出的就是0或1(军事,财经)
--------------------------------------------------------------------------------
类别数量:
1.二值分类
• Y的取值只有两种,如:email是否垃圾邮件
2.多值分类
• Y的取值大于两个,如:网页分类{政治,经济,体育,……}
类别关系:
1.水平关系
• 类别之间无包含关系
2.层级关系
• 类别形成等级体系
分类问题一般不考虑层级关系,聚类问题一般考虑层级关系
评估质量:
准确率,召回率,auc.....
什么决定了评估质量?
两个因素:
1.好的学习教材--------->数据---------->预处理(分词,TFIDF,离散化,连续值)
2.好的学习方法--------->算法
分类任务的解决流程:
假设:新闻分类
1.特征表示:x={昨日,是,国内,投资,市场……} x表示文章(学习的教材),然后分词
2.特征选择:X={国内,投资,市场……} 把好的特征留下来
3.模型选择:朴素贝叶斯分类器 (学习方法)
4.训练数据准备
5.模型训练
6.预测(分类)
7.评测
分类算法的大致分类:
1.概率分类器
– NB
– 计算待分类对象属于每个类别的概率,选择概率最大的类别作为最终输出
2.空间分割
– SVM
3.其他
– KNN
KNN很特别,其他的算法都是训练+预测,KNN是直接预测,但是计算量非常大
---------------------------------------------------------------------------------------------------------------
朴素贝叶斯:
- 概率模型
- 基于贝叶斯原理
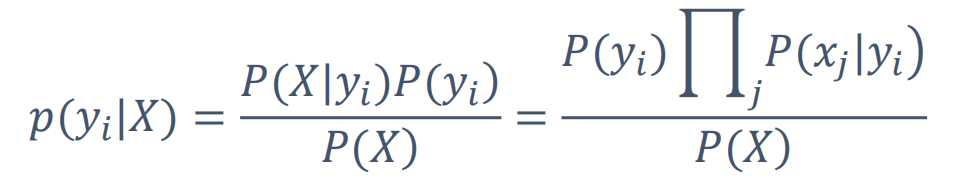
假设x是一片文章,yi就是什么类别(军事,财经...)的概率
• P(X):待分类对象自身的概率,可忽略
假设有1w篇文章,那文章自身的概率就是1/1w,每篇都是一样,所以可以忽略
• P(yi):每个类别的先验概率,如P(军事)
在训练之前就可以得到的一个值
假设有100片文章
30---军事 50---财经 20---生活
yi(军事 | 财经 | 生活)
p(军事)=30/100
p(财经)=50/100
p(生活)=20/100
• P(X|yi):每个类别产生该对象的概率
假设一篇文章x分成了n个单词x1,x2....xn
那么yi(一个类别)产生一片文章的概率,可以近似的看成yi产生一个词语的概率(x1,x2,x3...)
这篇文章包含所有的词语的话,对所有的词语做一个乘积(x1|yi)*(x2|yi)....(x3|yi)
所以
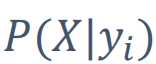 =
=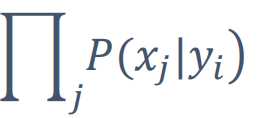
公式中每一项是怎么计算的?
策略:最大似然估计(maximum likehood estimation,MLE)
– P(Yi)
• Count(yi):类别为yi的对象在训练数据中出现的次数
例如:
• 总共训练数据1000篇,其中军事类300篇,科技类240篇,生活类140篇,……
• P(军事)=0.3, P(科技)=0.24, P(生活)=0.14,……
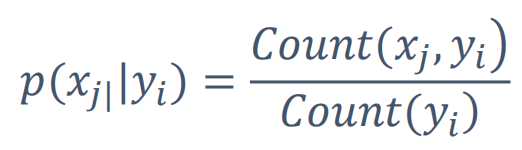
– P(xj|yi)
• Count(xj, yi):特征xj和类别yi在训练数据中同时出现的次数
– 例如:
• 总共训练数据1000篇,其中军事类300篇,科技类240篇,生活类140篇,……
• 军事类新闻中,谷歌出现15篇,投资出现9篇,上涨出现36篇
Count(yi):军事文章的和为300
Count(xj, yi):既是军事又出现了谷歌这个词的文章15/300=0.05
• P(谷歌|军事)=0.05, P(投资|军事)=0.03, P(上涨|军事)=0.12,……
上面的每个值都能计算了,就可以计算出每一篇文章那个类别的概率最大,就可以预测出来了(预测值为概率最大的)
-----------------------------------------------------------------------------------------------------------------------------------------------------------
例如:
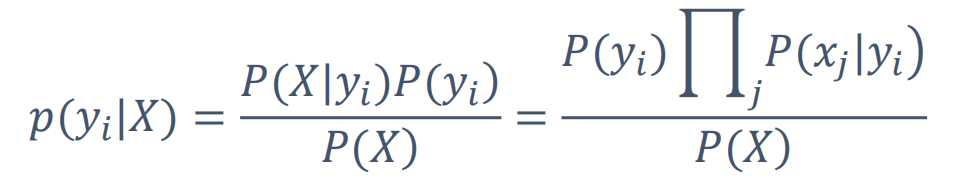
– 给定X,计算所有的p(yi|X),选择概率值最大的yi作为输出
• X={国内,投资,市场,……}
• P(军事|X)=P(国内|军事)* P(投资|军事)* P(市场|军事)……P(军事)
• 同样计算P(科技|X) P(生活|X)....
------------------------------------------------------------------------------------------------------------------------------------------------------------
评测指标怎么看?
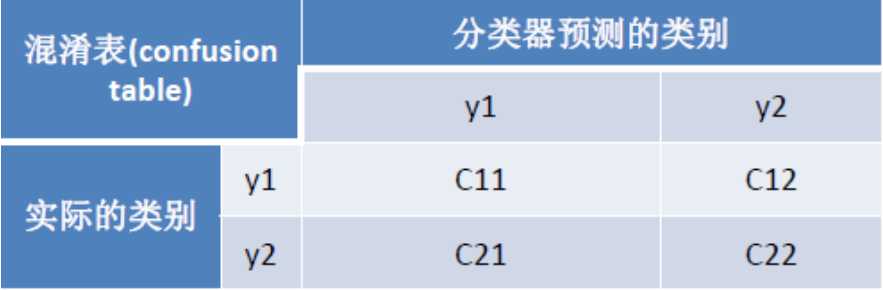
混淆表:
验证的时候是不能用测试集的,因为就是在测试集上做的
• 准确度Accuracy:(C11+C22)/(C11+C12+C21+C22)
• 精确率Precision(y1):C11/(C11+C21)
• 召回率Recall(y1):C11/(C11+C12)
例子:
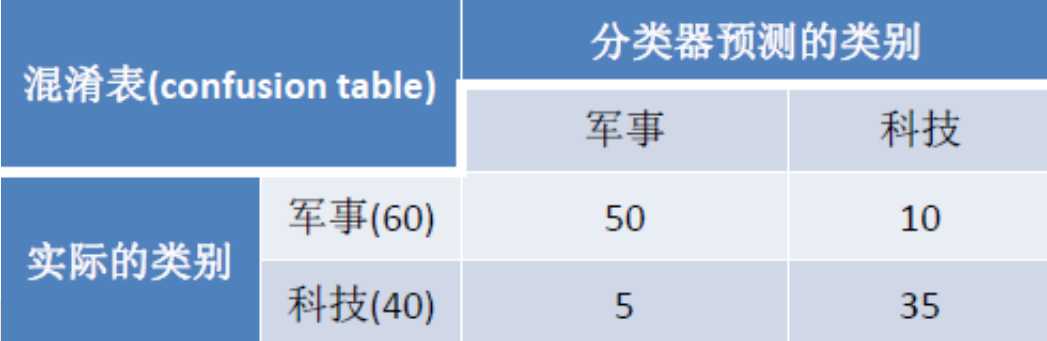
假设有100篇文章,但是在测试之前我们就知道有60篇是军事,40篇是科技
但是计算器反馈是50+5篇军事的,10+35篇科技的
• 准确度Accuracy:(50+35)/(35+5+10+50)=85%
• 精确率Precision(y1):50/(50+5)=90.9%
• 召回率Recall(y1):50/(50+10)=83.3%
一般精确率在70%以上就可以在线上使用了,但是不能只是精确率高召回率低或者精确率低召回率高
通常我们还得看一个指标:auc
auc:负样本排在正样本前面的概率(不太好演示....可以度娘)
auc计算: cat xxx | sort -k2g | awk ‘($1==0){++x;a+=y;}($2==1){++y;}END{print 1.0-a/(x*y)}‘
朴素贝叶斯:
优点:简单有效,结果是概率,对二值和多值同样适用(前提是分词一定要好,IFIDF权重一定要把握好)
缺点:独立性假设有时不合理
原文:https://www.cnblogs.com/fishperson/p/10506809.html